NCERT Solutions For Class 11 Maths chapter-9 Sequences And Series Exercise 9.1

NCERT Solutions For Class 11 Maths chapter-9 Sequences And Series Exercise 9.1

NCERT Solutions for Class-11 Maths Chapter-9 Sequences and Series

NCERT Solutions For Class 11 Maths Chapter-9 Sequences and Series Exercise 9.1 prepared by an expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download solution of all chapters from Physics Wallah NCERT solutions of class 11.

NCERT Solutions for Class-11 Maths Exercise 9.1

Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:

Question 1. Write the first five terms of the sequences whose n ^th term is a _n =n(n+2).

Solution :
a _n =n(n+2)

Substituting n = 1, 2, 3, 4, and 5, we obtain

a ₁ =1(1 + 2)=3

a ₂ =2(2 + 2)=8

a ₃ =3(3 + 2)=15

a ₄ =4(4 + 2)=24

a ₅ =5(5 + 2)=35

Therefore, the required terms are 3, 8, 15, 24, and 35.

Question 2. Write the first five terms of the sequences whose n ^th term is a n= n/n+1.

Solution :
Given: n= n/n+1.

Putting n = 1 and 5, we get,

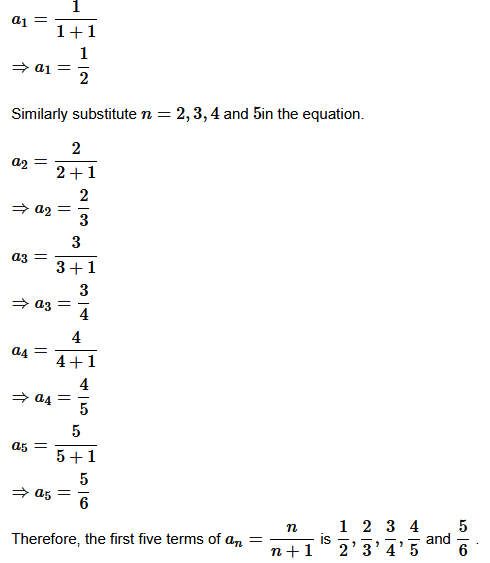
Question 3. a _n = 2 ⁿ

Solution :
Given:  n ^{th term , a _n = 2 n}

Putting n = 1,2,3,4,and 5, we get,

a ₁ = 2 ¹ = 2

a ₂ = 2 ² = 4

a ₃ = 2 ³ = 8

a ₄ = 2 ⁴ = 16

a ₅ = 2 ⁵ = 32

Therefore, the first five terms are 2, 4, 8, 16 and 32.

Question 4. a _n = (2n-3) / 6

Solution :
Given: a _n = (2n-3) / 6

Putting 1and 5, we get,

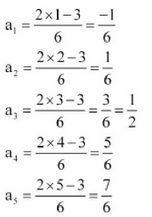
Therefore, the first five terms are -1/6, 1/6 , 1/2 , 5/6 and 7/6

Question 5. a ⁿ = (−1) ⁿ⁻¹ 5 ⁿ⁺¹

Solution :
Given: ⁿ = (−1) ⁿ⁻¹ 5 ⁿ⁺¹

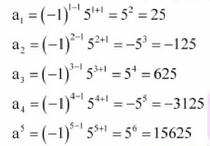
Therefore, the first five terms are 25, -125, 625, -3125 and 15625

Question 6. Write the first five terms of the sequences whose n ^th
term is

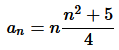
Solution :
Given:

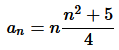
Putting n = 1 2,3,4 and 5, we get,

Find the indicated terms in each of the sequences in Exercises 7 to 10 where 17 ^th terms are:

Question 7. a _n =4 ⁿ⁻³ ;  a ₁₇ , a ₂₄

Solution :
Given: The given equation is a _n =4n−3

.

Substitute n=17

in the equation.

a ₁₇ =4(17)−3

⇒a ₁₇ =65

Similarly substitute n=24

in the equation.

a ₂₄ =4(24)−3

⇒a ₂₄ =93

Therefore, the 17th
and 24th
term of an=4n−3
is 65
and 93
respectively.

Question 8. a _n = n ² / 2 ⁿ ;a ₇

Solution :
Given:

The given equation is a _n = n ² /  2 ⁿ

.

Substitute n = 7 in the equation.

a ⁷ =  7227

⇒a ⁷ =  49128

Therefore, the 7 ^th
term of an=n ² /  2 ⁿ
is 49128

.

Question 9. a _n =(−1) ⁿ⁻¹ n ³ ;a ₉

Solution :
Given:

The given equation is a _n =(−1) ⁿ⁻¹ n ³

Substitute n=9

in the equation.

a ⁹ =   (−1) ⁹⁻¹ 9 ³

⇒a ⁹ =  729

Question 10.

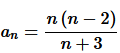
Solution :

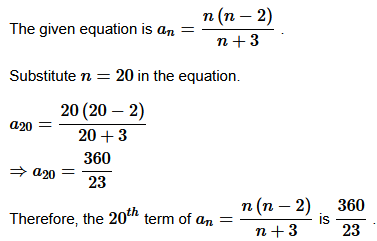
Write the first five terms of each of the sequences in Exercises 11 to 13 and obtain the corresponding series:

Question 11. a1 =3, a _n = 3a _n-1 + 2 for all n > 1

Solution :
Given: a1 =3, a _n = 3a _n-1 + 2 for all n > 1

Putting 1 ,2,3,4 and 5, we get

The given equation is a _n =  3a ⁿ⁻¹ +2
where a ₁ = 3
and n>1

.

Substitute n=2
and a ₁ = 3

in the equation.

a ₂ = 3a _{2 − 1} +2 =3(3) + 2

⇒ a ₂ =11

Similarly substitute n=3,4
and 5

in the equation.

a ₃ = 3a ₃ − 1 + 2=3(11)+2

⇒a ₃ = 35

a ₄ = 3a ₄ − 1+2 = 3(35)+2

⇒a ₄ = 107

a ₅ = 3a ₅₋₁ + 2 = 3(107)+2

⇒a ₅ = 323

Therefore, the first five terms of an=3a _n−1 +2
is 3,11,35,107
and 323

.

Question 12. Write the first five terms of the following sequence and obtain the corresponding series:

a ₁ = −1,a _n = a _n−1 / n, n≥2

Solution :
Given: a ₁ = −1,a _n = a _n−1 / n, n≥2

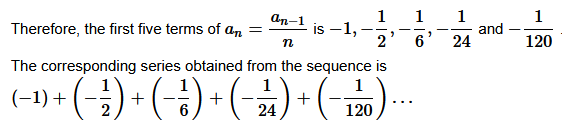
Question 13. Write the first five terms of the following sequence and obtain the corresponding series:

a ₁ = a _{2 =} 2, a _n = a _n−1 −1, n>2

Solution :
Given:

The given equation is a _n = a _n−1 −1
where a ₁ = a ₂ =2
and n>2

.

Substitute n=3
and a ₂ = 2

in the equation.

a ₃ =a ₃₋₁ − 1 = 2−1

⇒a ₃ = 1

Similarly substitute n=4
and 5

in the equation.

a ₄ = a ₄₋₁ −1 = 1−1

⇒a ₄ = 0

a = a ₅₋₁ −1 =  0−1

⇒a ₅ = −1

Therefore, the first five terms of a _n = a _n−1 −1
is 2,2,1,0
and −1

.

The corresponding series obtained from the sequence is 2+2+1+0+(−1)+...
.

Question 14. The Fibonacci sequence is defined by  1= a ₁ = a ₂ and a _n = a _n−1 + a _n−2 , n>2 Find a _n+1 / a _n , for n=1, 2, 3, 4, 5

Solution :
Given: 1= a ₁ = a ₂ and a _n = a _n−1 + a _n−2

Putting 1,2,3, 4, 5 and 6, we have

The given equation is an=an−1−1
where a1=a2=2
and n>2

.

Substitute n=3
and a2=2

in the equation.

a3=a3−1−1=2−1

⇒a3=1

Similarly substitute n=4
and 5

in the equation.

a4=a4−1−1=1−1

⇒a4=0

a5=a5−1−1=0−1

⇒a5=−1

Therefore, the first five terms of an=an−1−1
is 2,2,1,0
and −1