NCERT Solutions For Class 11 Maths chapter-9 Sequences And Series Exercise 9.2
NCERT Solutions for Class-11 Maths Chapter-9 Sequences and Series
NCERT Solutions For Class 11 Maths
Chapter-9 Sequences and Series Exercise 9.2 prepared by an expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download solution of all chapters from Physics Wallah
NCERT solutions
of class 11.
NCERT Solutions for Class-11 Maths Exercise 9.2
Write the first five terms of each of the sequences in Exercises 1 to 6 whose nth terms are:
Question
1. Find the sum of odd integers from 1 to 2001.
Solution :
Odd integers from 1 to 2001 are 1, 3, 5, 7, …….., 2001.
The first term of the A.P. is a=1
and the common difference is d=2
.
The n
th
term of the A.P. is given by the equation an=a+(n−1)d
.
Therefore, a+(n−1)d=2001
Substitute a=1
and d=2
in the equation.
⇒1+(n−1)2=2001
⇒2n−1=2001
⇒n=2001+1
/
2
⇒n=1001
The sum of first n
terms of an arithmetic progression is given by the equation
.
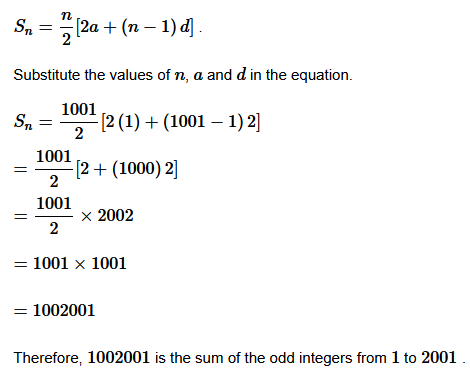
Question
2. Find the sum of all natural numbers lying between 100 and 1000 which are multiples of 5.
Solution :
105,110,...,990,995 are the natural numbers lying between 100
and 1000
, which are multiples of 5
. An A.P. is formed by this sequence.
The first term of the A.P. is a=105
and the common difference is d=5
.
The nth
term of the A.P. is given by the equation an=a+(n−1)d
.
Therefore, a+(n−1)d=995
Substitute a=105
and d=5
in the equation.
⇒105+(n−1)5=995
⇒5n+100=995
Question
3. In an A.P. the first term is 2 and the sum of the first five terms is one-fourth of the next five terms. Show that 20
th
term is -112.
Solution :
The first term of the A.P. is 2
and let the common difference of the A.P. be d
.
Then 2,2+d,2+2d,2+3d,...
is the A.P.
10+10d
is the sum of the first five terms and 10+35d
is the sum of the next five terms.
According to the conditions given in the question,
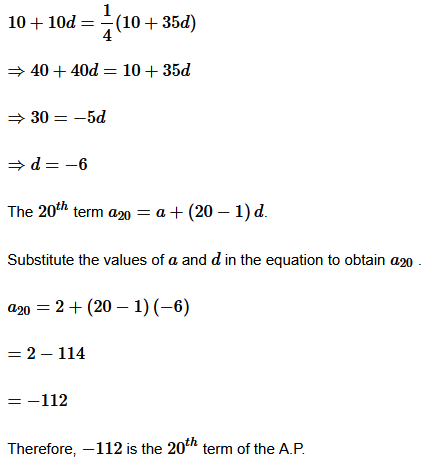
Question
4. How many terms of the A.P., -6, -11/2 ,-5 ................ are needed to give the sum -25.?
Solution :
⇒ n = 20 ,5
There for , 5 or 20 terms of the Ap are needed to give he sum - 25 .
Question
5. In an A.P., if pth term is 1/q and qth term is 1/p , prove that the sum of first pq terms is 1/2(pq+1), where p≠q
Solution :
The sum of first n terms of an arithmetic progression is given by the equation
Question
6. If the sum of a certain number of terms of the A.P. 25, 22, 19, ….. is 116, find the last term.
Solution :
Here116 is the sum of n
terms of the given A.P.
The common difference of the A.P. is d=22−25=−3
The sum of first n
terms of an arithmetic progression is given by the equatio
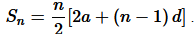
Substitute Sn=116
, a=25
and d=−3
in the equation.
116=n / 2[2(25)+(n−1)−3]
⇒232=n[50+−3n+3]
⇒232=n(53−3n)
⇒3n
2
−53n+232=0
Factorize the equation.
⇒3n
2
−24n−29n+232=0
⇒3n(n−8)−29(n−8)=0
⇒(n−8)(3n−29)=0
⇒n=8 or 29 /3
n=8 as n cannot be equal to 29 / 3
As n=8 the last term is
a
8
= a + (8−1)d
Substitute a=25 and d=−3
in the equation.
a
8
= 25+(7)(−3)
=25−21
=4
Therefore, 4 is the last term of the A.P.
Question
7. Find the sum to n terms of the A.P., whose k
th
term is 5k + 1.
Solution :
5k+1 is given as the k
th
term of the A.P. The equation for kth
term of an A.P. is given as ak+(k−1)d
.Then,
a+(k−1)d = 5k + 1
⇒a + kd − d = 5k + 1
By comparing the coefficient of k we get the value of d as 5
⇒a−d=1
⇒a−5=1
⇒a=6
The sum of first n
terms of an arithmetic progression is given by the equation
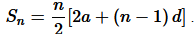
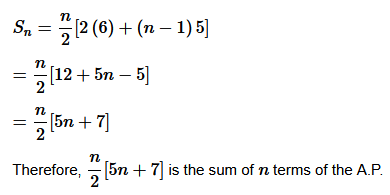
Question
8. If the sum of n terms of an A.P. is (pn + qn
2
) where p and q are constants,find the common difference.
Solution :
Given:
(pn + qn
2
)
The sum of first n terms of an arithmetic progression is given by the equation
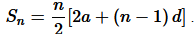
Question
9. The sums of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 18
th
terms.
Solution :
Let a1 and d1 be the first term and the common difference of the first arithmetic progression respectively and a2 and d2 be the first term and the common difference of the second arithmetic progression respectively.
hbAccording to the conditions given in the question, Sum of n terms of first A.P / Sum of n terms of second A.P.
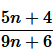
Therefore, the ratio of 18
th
terms of two A.P.’s is 179: 321.
Question
10. If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.
Solution :
Let a
be the first term and d
be the common difference of the A.P.
The sum of first p
terms of the A.P. is given by the equation
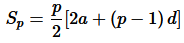and
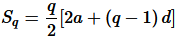
= P+q / 2[2a -2a ]
= 0
= Therefore, 0 is the sum of the first (p+q) terms of the A.P.
Question
11. Sum of the first p, q and r terms of an A.P. are a, b and c, respectively. Prove that a/p (q−r) + b/q(r−p) + c/r(p−q) = 0.
Solution :
Let A be the first term and
d
be the common difference of given A.P.
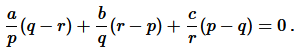
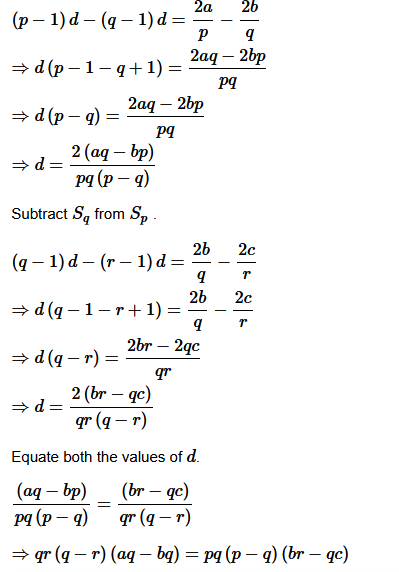
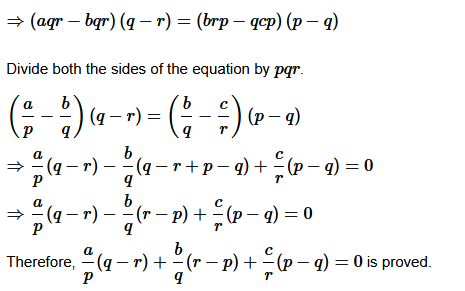
L.H.S. = R.H.S. Proved.
Question
12. The ratio of the sums of m and n terms of an A.P. is m
2
: n
2
. Show that the ratio of m
th
and n
th
term is (2m – 1) : (2n – 1).
Solution :
Let
a
be the first term and
d
be the common difference of given A.P.
Let a be the first term of the A.P. and d be the common difference. According to the conditions given in the question, Sum of m terms / Sum of n termsand m
2
/ n
2
Question
13.If the sum of n terms of an A.P. is 3n
2
+ 5n and its mth term is 164, find the value of m.
Solution :
:
Question
14. Insert five numbers between 8 and 26 so that the resulting sequence is an A.P.
Solution :
Let the five numbers between 8
and 26
be A
1
,A
2
,A
3
,A
4
and A
5
. Then the resulting sequence 8,A
1,
A
2
,A
3
,A
4,
A
5
,26
is an A.P.
The first term of the A.P. a=8
, the last term b=26
and the number of terms n=7
.
Substitute the values of a,b
and n
in b=a+(n−1)d
.
⇒26=8+(7−1)d
⇒6d=26−8
⇒d=3
Then substituting the values of a
and d
we get
A
1
=a+d=8+3=11
A
2
=a+2d=8+2(3)=14
A
3
=a+3d=8+3(3)=17
A
4
=a+4d=8+4(3)=20
A
5
=a+5d=8+5(3)=23
Therefore, 11,14,17,20
and 23
are the five numbers between 8
and 26
Question
15. If
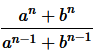is the A.M. between a and b then find the value of n.
Solution :
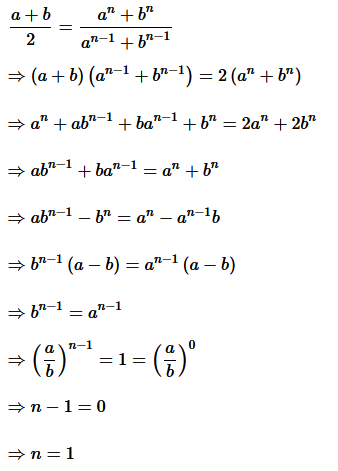
Question
16. Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A. P. and the ratio of 7
th
and (m–1)
th
numbers is 5 : 9. Find the value of m.
Solution :
Let A. P a
1
, A
2
, A
3
, A
4
, …….., A
m
be n = m + 2 numbers between 1 and 31.
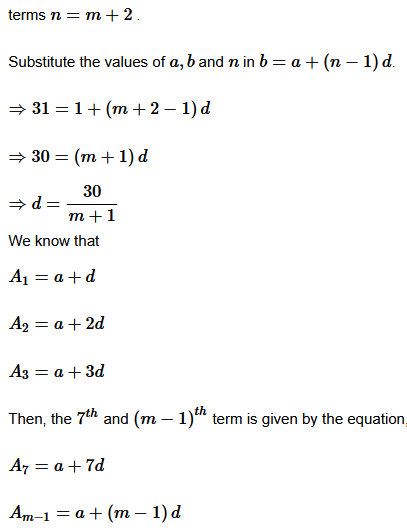
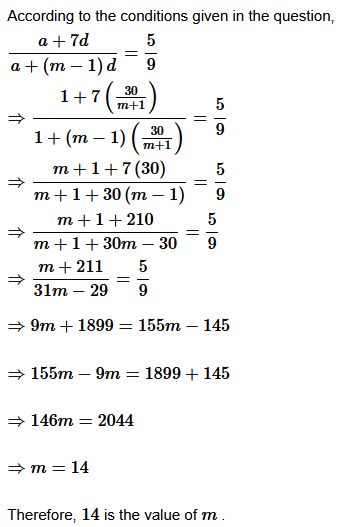
Question
17. A man starts repaying a loan as first installment of Rs. 100. If he increases the installment by Rs. 5 every month, what amount he will pay in the 30
th
installment?
Solution :
Amount of 1st installment = Rs. 100 and Amount of 2nd installment = Rs. 105
Rs.100
is the first installment of the load and Rs.105
is the second installment and so on.
Therefore, an A.P. is formed by the amount that the man repays every month.
100,105,110...
is the A.P.
The first term of the A.P. a=100
and the common difference d=5
The 30
th
is given by the equation A30=a+(30−1)d
.
⇒A
30
= 100+(29)
5
=100+145
=245
Therefore, Rs.245
is the amount to be paid in the 30th
installment.= Rs. 245
Therefore, the amount of 30th installment is Rs. 245.
Question
18. The difference between any two consecutive interior angles of a polygon is 5
º
If the smallest angle is 120
º
find the number of the sides of the polygon.
Solution :
An A.P. is formed by the angles of the polygon. The first term of the A.P. a = 120
∘
and the common difference d = 5
∘
.
We know that 180(n−2)
is the sum of all angles of a polygon with n
sides.
Therefore, S
n
= 180
∘
(n−2)
⇒n/2 [2a+(n−1)d] = 180
∘
(n−2)
⇒n/2[240
∘
+(n−1)5
∘
] = 180
∘
(n−2)
⇒n[240+(n−1)
5
] = 360(n−2)
⇒240n+5n
2
−5n=360n−720
⇒5n
2
−125n+720=0
⇒n
2
− 25n + 144=0
⇒n
2
− 16n−9n+144=0
⇒n(n−16)−9(n−16)=0
⇒(n−9)(n−16)=0
⇒n=9
or 16
Therefore, the number of the sides of the polygon 9
or 16
