NCERT Solutions For Class 11 Maths chapter 16-Probability Exercise 16.3

NCERT Solutions For Class 11 Maths chapter 16-Probability Exercise 16.3

NCERT Solutions for Class-11 Maths Chapter-16 Probability

Academic team of Physics Wallah developed step by step NCERT Solutions for Class-11 Maths Chapter-16 Probability (Ex 16.3) Exercise 16.3 according to recommendations and Guideline of CBSE Read chapter-1 theory make sure you have gone through the theory part of Chapter-16 Probability from NCERT textbook and you have learned the formula of the given chapter. You can download and share NCERT Solutions for Class 11 Maths.

NCERT Solutions for Class-11 Maths Exercise 16.3

Question 1. Which of the following can not be valid assignment of probabilities for outcomes of sample space S =

Solution :
(a)

Here, each of the numbers p(ω _i ) is positive and less than 1.

Sum of probabilities

0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1

Thus, the assignment is valid.

(b)

Here, each of the numbers p(ωi) is positive and less than 1.

Sum of probabilities

= (1/7) + (1/7) + (1/7) + (1/7) + (1/7) + (1/7) + (1/7)

= 7/7

= 1

Thus, the assignment is valid.

(c)

Here, each of the numbers p(ωi) is positive and less than 1.

Sum of probabilities

= 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7

= 2.8 > 1

Therefore, the 2 ^nd condition is not satisfied

Which states that p(w _i ) ≤ 1

Thus, the assignment is not valid.

(d)

Here, p(ω ₁ ) and p(ω ₅ ) are negative.

Hence, the assignment is not valid.

(e)

Here,Sum of probabilities

= (1/14) + (2/14) + (3/14) + (4/14) + (5/14) + (6/14) + (7/14)

= (28/14) ≥ 1

Hence, the assignment is not valid.

Question 2. A coin is tossed twice, what is the probability that at least one tail occurs?

Solution :
When a coin is tossed twice, the sample space is given by

S = {HH, HT, TH, TT}

∴ Number of possible outcomes n (S) = 4

Let A be the event of the occurrence of at least one tail.

Accordingly, A = {HT, TH, TT}

∴ n (A) = 3

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

P(A) = n(A)/n(S)

= ¾

Question 3. A die is thrown, find the probability of following events:

(i) A prime number will appear,

(ii) A number greater than or equal to 3 will appear,

(iii) A number less than or equal to one will appear,

(iv) A number more than 6 will appear,

(v) A number less than 6 will appear.

Solution :
The sample space of the given experiment is given by

S = {1, 2, 3, 4, 5, 6}

∴n(S) = 6

(i) Let A be the event of the occurrence of a prime number.

Accordingly, A = {2, 3, 5}

Then, n(A) = 3

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(A) = n(A)/n(S)

= 3/6

= ½

(ii) Let B be the event of the occurrence of a number greater than or equal to 3. Accordingly, B = {3, 4, 5, 6}

Then, n(B) = 4

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(B) = n(B)/n(S)

= 4/6

= 2/3

(iii) Let C be the event of the occurrence of a number less than or equal to one. Accordingly, C = {1}

Then, n (C) = 1

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(C) = n(C)/n(S)

= 1/6

(iv) Let D be the event of the occurrence of a number greater than 6.

Accordingly, D = 0

Then, n (D) = 0

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(D) = n(D)/n(S)

= 0/6

= 0

(v) Let E be the event of the occurrence of a number less than 6.

Accordingly, E = {1, 2, 3, 4, 5}

Then, n (E) = 5

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(E) = n(E)/n(S)

= 5/6

Question 4. A card is selected from a pack of 52 cards.

(a) How many points are there in the sample space?

(b) Calculate the probability that the card is an ace of spades.

(c) Calculate the probability that the card is (i) an ace (ii) black card.

Solution :

From the question it is given that, there are 52 cards in the deck.

(a) Number of points in the sample space = 52 (given)

∴n(S) = 52

(b) Let us assume ‘A’ be the event of drawing an ace of spades.

A= 1

Then, n (A) = 1

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(A) = n(A)/n(S)

= 1/52

(c) Let us assume ‘B’ be the event of drawing an ace. There are four aces.

Then, n (B)= 4

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(B) = n(B)/n(S)

= 4/52

= 1/13

(d) Let us assume ‘C’ be the event of drawing a black card. There are 26 black cards.

Then, n (C) = 26

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(C) = n(C)/n(S)

= 26/52

= ½

Question 5. A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12

Solution :

Let us assume that 1, 2, 3, 4, 5 and 6 are the possible out comes when the die is thrown.

So, the sample space S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5),(6, 6)}

Then, n(S) = 12

(i) Let us assume ‘P’ be the event having sum of numbers as 3.

P = {(1, 2)},

Then, n (P) = 1

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(P) = n(P)/n(S)

= 1/12

(ii) Let us assume ‘Q’ be the event having sum of number as 12.

Then Q = {(6, 6)}, n (Q) = 1

P(Event) = Number of outcomes favorable to event/ Total number of possible outcomes

∴P(Q) = n(Q)/n(S)

= 1/12

Question 6. There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?

Solution :
There are four men and six women on the city council.

As one council member is to be selected for a committee at random, the sample space contains 10 (4 + 6) elements.

Let A be the event in which the selected council member is a woman.

Accordingly, n(A) = 6

P(Event) = Number of outcomes favourable to event/Total number of possible outcomes

∴P(A) = n(A)/n(S)

= 6/10 … [divide both numerator and denominators by 2]

= 3/5

Question 7. A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.

Solution :
Since the coin is tossed four times, there can be a maximum of 4 heads or tails.

When 4 heads turns up, Re 1 + Re 1 + Re 1 + Re 1 = Re 4 is the gain.

When 3 heads and 1 tail turn up, Re 1 + Re 1 + Re 1 – Rs 1.50 = Rs 3 – Rs 1.50 = Rs 1.50 is the gain.

When 2 heads and 2 tails turns up, Re 1 + Re 1 – Rs 1.50 – Rs 1.50 = – Re 1, i.e., Re 1 is the loss.

When 1 head and 3 tails turn up, Re 1 – Rs 1.50 – Rs 1.50 – Rs 1.50 = – Rs 3.50, i.e., Rs 3.50 is the loss.

When 4 tails turn up, – Rs 1.50 – Rs 1.50 – Rs 1.50 – Rs 1.50 = – Rs 6.00, i.e., Rs 6.00 is the loss.

There are 24 = 16 elements in the sample space S, which is given by:

S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTTH, TTHH, HTHT, THTH, THHT, HTTT, THTT, TTHT, TTTH, TTTT}

∴n(S) = 16

The person wins Rs 4.00 when 4 heads turn up, i.e., when the event {HHHH} occurs.

∴Probability (of winning Rs 4.00) =1/16

The person wins Rs 1.50 when 3 heads and one tail turn up, i.e., when the event {HHHT, HHTH, HTHH, THHH} occurs.

∴Probability (of winning Rs 1.50) =4/16 = 1/6

The person loses Re 1.00 when 2 heads and 2 tails turn up, i.e., when the event {HHTT, HTTH, TTHH, HTHT, THTH, THHT} occurs.

∴Probability (of losing Re 1.00) = 6/16 = 3/8

The person loses Rs 3.50 when 1 head and 3 tails turn up, i.e., when the event {HTTT, THTT, TTHT, TTTH} occurs.

Probability (of losing Rs 3.50) =4/16 = 1/4

The person loses Rs 6.00 when 4 tails turn up, i.e., when the event {TTTT} occurs.

Probability (of losing Rs 6.00) = 1/16

Question 8. Three coins are tossed once. Find the probability of getting

(i) 3 heads (ii) 2 heads (iii) at least 2 heads

(iv) at most 2 heads (v) no head (vi) 3 tails

(vii) exactly two tails (viii) no tail (ix) at most two tails.

Solution :

Since either coin can turn up Head (H) or Tail (T), are the possible outcomes.

But, now three coin is tossed so the possible sample space contains,

S = {HHH, HHT, HTH, THH, TTH, HTT, TTT, THT}

Where s is sample space and here n(S) = 8

(i) 3 heads

Let us assume ‘A’ be the event of getting 3 heads

n(A)= 1

∴P(A) = n(A)/n(S)

= 1/8

(ii) 2 heads

Let us assume ‘B’ be the event of getting 2 heads

n (A) = 3

∴P(B) = n(B)/n(S)

= 3/8

(iii) at least 2 heads

Let us assume ‘C’ be the event of getting at least 2 head

n(C) = 4

∴P(C) = n(C)/n(S)

= 4/8

= ½

(iv) at most 2 heads

Let us assume ‘D’ be the event of getting at most 2 heads

n(D) = 7

∴P(D) = n(D)/n(S)

= 7/8

(v) no head

Let us assume ‘E’ be the event of getting no heads

n(E) = 1

∴P(E) = n(E)/n(S)

= 1/8

(vi) 3 tails

Let us assume ‘F’ be the event of getting 3 tails

n(F) = 1

∴P(F) = n(F)/n(S)

= 1/8

(vii) Exactly two tails

Let us assume ‘G’ be the event of getting exactly 2 tails

n(G) = 3

∴P(G) = n(G)/n(S)

= 3/8

(viii) no tail

Let us assume ‘H’ be the event of getting no tails

n(H) = 1

∴P(H) = n(H)/n(S)

= 1/8

(ix) at most two tails

Let us assume ‘I’ be the event of getting at most 2 tails

n(I) = 7

∴P(I) = n(I)/n(S)

= 7/8

Question 9. If 2/11 is the probability of an event, what is the probability of the event ‘not A’.

Solution :
It is given that P(A) =2/11.

Accordingly, P(not A) = 1 – P(A)

= 1 – (2/11)

= (11 – 2)/11

= 9/11

10. A letter is chosen at random from the word ‘ASSASSI NATION’. Find the probability that letter is (i) a vowel (ii) an consonant

Solution :
There are 13 letters in the word ASSASSI NATION.

∴Hence, n(S) = 13

(i) There are 6 vowels in the given word.

n(A) = 6

∴P(A) = n(A)/n(S)

= 6/13

(ii) There are 7 consonants in the given word.

n(B)= 7

∴P(B) = n(B)/n(S)

= 7/13

Question 11. In a lottery, person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? [Hint: order of the numbers is not important.]

Solution :
Total number of ways in which one can choose six different numbers from 1 to 20

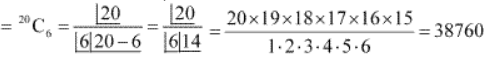
Hence, there are 38760 combinations of 6 numbers.

Out of these combinations, one combination is already fixed by the lottery committee.

∴ Required probability of winning the prize in the game =

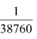
Question 12. Check whether the following probabilities P(A) and P(B) are consistently defined

(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6

(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8

Solution :
(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6

It is known that if E and F are two events such that E ⊂ F, then P(E) ≤ P(F).

However, here, P(A ∩ B) > P(A).

Hence, P(A) and P(B) are not consistently defined.

(ii)P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8

It is known that if E and F are two events such that E ⊂ F, then P(E) ≤ P(F).

Here, it is seen that P(A ∪ B) > P(A) and P(A ∪ B) > P(B).

Hence, P(A) and P(B) are consistently defined.

Question 13. Fill in the blanks in following table:

Solution :

(i) P(A) = 1/3, P(B) = 1/5, P(A ∩ B) = 1/15, P(A ∪ B) = ?

We know that,

P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

= (1/3) + (1/5) – (1/15)

= ((5 + 3)/15) – (1/15)

= (8/15) – (1/15)

= (8 – 1)/15

= 7/15

(ii) Here, P(A) = 0.35, P(A ∩ B) = 0.25, P(A ∪ B) = 0.6

We know that P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

∴0.6 = 0.35 + P(B) – 0.25

⇒ P(B) = 0.6 – 0.35 + 0.25

⇒ P(B) = 0.5

(iii)Here, P(A) = 0.5, P(B) = 0.35, P(A ∪ B) = 0.7

We know that P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

∴0.7 = 0.5 + 0.35 – P(A ∩ B)

⇒ P(A ∩ B) = 0.5 + 0.35 – 0.7

⇒ P(A ∩ B) = 0.15

Question 14. Given P(A) = 5/3 and P(B) = 1/5 . Find P(A or B), if A and B are mutually exclusive events.

Solution :
Here, P(A) =5/3, P(B) =1/5

For mutually exclusive events A and B,

P(A or B) = P(A) + P(B)

∴ P(A or B), if A and B are mutually exclusive

P(A∪B) or P(A or B) = P(A) + P(B)

= (3/5) + (1/5)

= 4/5

Question 15. If E and F are events such that P(E) = 1/4 , P(F) = 1/2 and P(E and F) = 1/8 , find:(i) P(E or F), (ii) P(not E and not F).

Solution :
Here, P(E) = 1/4, P(F) = 1/2, and P(E and F) =1/8

(i) We know that P(E or F) = P(E) + P(F) – P(E and F)

∴P(E or F) = ¼ + ½ – (1/8)

= 5/8

(ii)

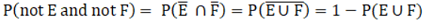
= 1 – (5/8)

= (8 – 5)/8

= 3/8

Question 16. Events E and F are such that P(not E or not F) = 0.25, State whether E and F are mutually exclusive.

Solution :
It is given that P (not E or not F) = 0.25

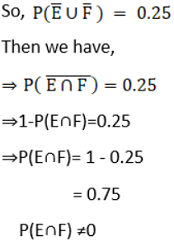
Thus, E and F are not mutually exclusive.

Question 17. A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. Determine (i) P(not A), (ii) P (not B) and (iii) P(A or B).

Solution :
It is given that P(A) = 0.42, P(B) = 0.48, P(A and B) = 0.16

(i) P(not A) = 1 – P(A) = 1 – 0.42 = 0.58

(ii) P(not B) = 1 – P(B) = 1 – 0.48 = 0.52

(iii) We know that P(A or B) = P(A) + P(B) – P(A and B)

∴ P(A or B) = 0.42 + 0.48 – 0.16 = 0.74

Question 18. In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.

Solution :
Let A be the event in which the selected student studies Mathematics and B be the event in which the selected student studies Biology.

Accordingly, P(A) = 40% = 40/100= 2/5

P(B) = 30% = 30/100 = 3/10

P(A and B) = 10% = 10/100 = 1/10

We know that P(A or B) = P(A) + P(B) – P(A and B)

P(A or B) = 2/5 + 3/10 - 1/10 = 6/10

Thus, the probability that the selected student will be studying Mathematics or Biology is 0.6.

Question 19. In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing at least one of them is 0.95. What is the probability of passing both?

Solution :
Let A and B be the events of passing first and second examinations respectively.

Accordingly, P(A) = 0.8, P(B) = 0.7 and P(A or B) = 0.95

We know that P(A or B) = P(A) + P(B) – P(A and B)

∴0.95 = 0.8 + 0.7 – P(A and B)

⇒ P(A and B) = 0.8 + 0.7 – 0.95 = 0.55

Thus, the probability of passing both the examinations is 0.55.

Question 20. The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?

Solution :
Let A and B be the events of passing English and Hindi examinations respectively.

Here given, P(A) = 0.75, P(A∩B) – 0.5, P(A ^I ∩B ^I ) = 0.1

We know that, P(A ^I ∩B ^I ) = 1 – P(A∪B)

Then, P(A∪B) = 1 – P(A ^I ∩B ^I )

= 1 – 0.1

= 0.9

We know that P(A or B) = P(A) + P(B) – P(A and B)

∴0.9 = 0.75 + P(B) – 0.5

⇒ P(B) = 0.9 – 0.75 + 0.5

⇒ P(B) = 0.65

Thus, the probability of passing the Hindi examination is 0.65.

Question 21. In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that

(i) The student opted for NCC or NSS.

(ii) The student has opted neither NCC nor NSS.

(iii) The student has opted NSS but not NCC.

Solution :

From the question it is given that,

The total number of students in class = 60

Thus, the sample space consist of n(S) = 60

Let us assume that the students opted for NCC be ‘A’

And also assume that the students opted for NSS be ‘B’

So, n(A) = 30, n(B) = 32 , n(A∩B) = 24

We know that, P(A) = n(A)/n(S)

= 30/60

= ½

P(B) = n(B)/n(S)

= 32/60

= 8/15

P(A∩B) = n(A∩B)/n(S)

= 24/60

= 2/5

Therefore, P(A∪B) = P(A) + P(B) – P(A∩B)

(i) The student opted for NCC or NSS.

P (A or B) = P(A) + P(B) –P(A and B)

P(A∪B) = P(A) + P(B) – P(A∩B)

= ½ + (8/15) – (2/5)

= 19/30

(ii) P(student opted neither NCC nor NSS)

P(not A and not B) = P(A ^I ∩B ^I )

We know that, P(A ^I ∩B ^I ) = 1 – P(A∪B)

= 1 – (19/30)

= 11/30

(iii) P(student opted NSS but not NCC)

n(B – A) = n(B) – n (A∩B)

⇒ 32 – 24 = 8

The probability that the selected student has opted for NSS and not NCC is

= (8/60) = 2/15