NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Exercise 8.2

NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Exercise 8.2

NCERT Solutions for Class-11 Maths Chapter-8 Binomial Theorem

NCERT Solutions For Class 11 Maths Chapter-8 Binomial Theorem Exercise 8.2 prepared by the expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download solution of all chapters from Physics Wallah NCERT solutions of class 11.

NCERT Solutions for Class-11 Maths Exercise 8.2

Find the coefficient of:

Question 1. Find the coefficient of x ⁵ in (x + 3) ⁸

Solution : It is known that (r+1) ^th term, (T _r+1 ). in the binomial expansion of (a+b) ⁿ is given by T _r+1 = ⁿ C _r a ^n−r b ^r

Assuming that x ²
occurs in the (r+1) ⁿ term of the expansion (x+3) ⁸ , we obtain T _^r+1 = ^a C _r (x) ^8-r (3) ^r

Comparing the indices of x
in x5 in T _r+1 . We obtain r = 3 Thus, the coefficient of x ⁵ is ⁸ C ₃ (3) ³ =8! / 3!5!×3 ³

=(8⋅7⋅6⋅5!  /  3⋅2.5!)∗3 ³ =1512

Question 2. Find the coefficient of a ⁵ b ⁷ in (a – 2b) ¹²

Solution :
General form of the expansion ( r + 1) ^th is (T _r+2 )………(i)

Write the general term in the expansion of

Question 3. Write the general term in the expansion of (x ² – y) ⁶

Solution :
It is known that the general term T _r+1 { which is the (r+1) ⁿ term } in the binomial expansion of (a+b)n is given by T _r+1 = ⁿ C _r a ^{n -r} b ^r .

Thus, the general term in the expansion of (x ² −y ⁶ )
is T _r+1 = ⁶ C _r (x ² ) ^6−r (−y) ^r = (−1) ^r6 C _r - x ^{12 −2r} ⋅y ^r

Question 4. Write the general term in the expansion of (x ² – yx) ¹² , x ≠ 0

Solution :
General form of the expansion T _r+1 is

{ which is the (r+1)th term } in the binomial expansion of (a+b)n is given by Tr+1=nCran−rbr.

Thus, the general term in the expansion of (x2−yx)12
is T _r+1 = ¹² C _r (x ² ) ^12−t (−yx) ^r

=(−1) ^r12 C _r −x ^24−2r −y ^r

=(−1) ^r−2 C _r x ^24−r⋅ y ^r

Question 5. Find the 4 ^th term in the expansion of (x – 2y) ¹² .

Solution :
It is known (r+1) ⁿ term, T _r+1 . in the binomial expansion of (a+b) ⁿ

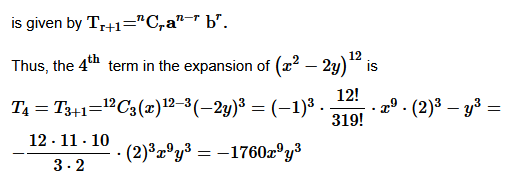
Question 6. Find the 13 ^th term in the expansion of

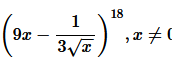
Solution :
It is known (r+1) ^th term, T _r+1 , in the binomial expansion of (a+b) ⁿ is given by T _ε+1 = ⁿ C _r a ⁿ⁻¹ b ^r

Thus, the 13 ^th
term in the expansion of

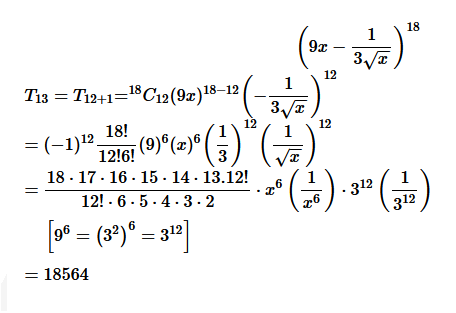
Find the middle terms in the expansion of:

Question 7.

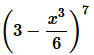
Solution :

Question 8. (x/3 + 9y) ¹⁰

Solution :
Here (a + b ) ⁿ which is an even number.

Therefore, the middle terms are (x/3 + 9y) ¹⁰ is 6th term.

General form of the expansion

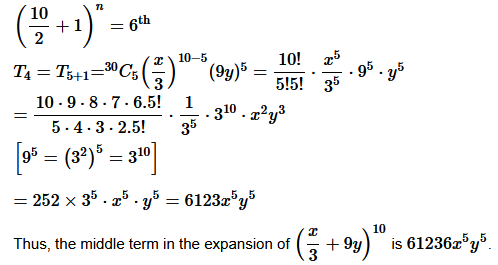
Question 9. In the expansion of (1 + a) ^{m + n} , prove that coefficients of am and an are equal.

Solution :

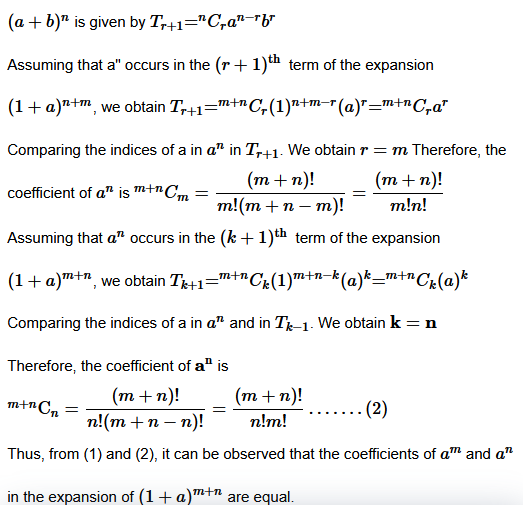
Question 10. The coefficients of the (r – 1) ^th , r ^th and (r + 1) ^th terms in the expansion of (x + 1) ⁿ are in the ratio 1:3:5. Find n and r.

Solution :

Question 11.  Prove that the coefficient of xn in the expansion of (1 + x) ²ⁿ is twice the coefficient of xn in the expansion of (1 + x) ^2n–1 .

Solution :

= It is known that (r+1) ^th term, (T _r+1 ), in the binomial expansion of (a+b) ⁿ is given by T _r+1 = ⁿ C _r a ^n−r b ^r

Assuming that x ⁿ
occurs in the (r+1) ⁿ term of the expansion of (1+x) ²ⁿ , we obtain T _r+1 = ²ⁿ Cr(1) ^2n−r (x) ^r

= ²ⁿ C _r (x) ^r

Comparing the indices of x
in xn and in T _r+1 , we obtain r=n Therefore, the coefficient of xn in the expansion of (1+x) ²ⁿ is