NCERT Solutions For Class 11 Maths chapter-12 Introduction to Three Dimensional Geometry Miscellaneous Exercise

NCERT Solutions for Class 11 Maths Chapter-12 Introduction to Three Dimensional Geometry

Academic team of Physics Wallah developed step by step NCERT Solutions for Class 11 Maths Chapter-12 Introduction to Three Dimensional Geometry Miscellaneous Exercise according to recommendations and Guideline of CBSE. You can download and share NCERT Solutions for Class 11 Maths.

NCERT Solutions for Class 11 Maths Miscellaneous Exercise

Question1. Three vertices of a parallelogram ABCD are A (3, –1, 2), B (1, 2, –4) andC (–1, 1, 2). Find the coordinates of the fourth vertex.

Solution :
The three vertices of a parallelogram ABCD are given as A (3, –1, 2), B (1, 2, –4), and C (–1, 1, 2). Let the coordinates of the fourth vertex be D (x,y,z).

We know that the diagonals of a parallelogram bisect each other.

Therefore, in parallelogram ABCD, AC and BD bisect each other.

∴Mid-point of AC = Mid-point of BD

⇒x = 1,y = –2, andz = 8

Thus, the coordinates of the fourth vertex are (1, –2, 8).

Question2. Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0).

Solution :
Let AD, BE, and CF be the medians of the given triangle ABC.

Since AD is the median, D is the mid-point of BC.

∴Coordinates of point D == (3, 2, 0)

Thus, the lengths of the medians of ΔABC are.

Question3. If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10) and R (8, 14, 2c), then find the values ofa,b andc.

Solution :

It is known that the coordinates of the centroid of the triangle, whose vertices are (x₁,y₁,z₁),  (x₂,y₂,z₂) and (x₃,y₃,z₃), are.

Therefore, coordinates of the centroid of ΔPQR

It is given that origin is the centroid of ΔPQR.

Thus, the respective values ofa,b, andc are

Question4. Find the coordinates of a point ony-axis which are at a distance of from the point P (3, –2, 5).

Solution :

If a point is on the y-axis, then x-coordinate and the z-coordinate of the point are zero.

Let A (0, b, 0) be the point on the y-axis at a distance of from point P (3, –2, 5). Accordingly,

Thus, the coordinates of the required points are (0, 2, 0) and (0, –6, 0).

Question5. A point R withx-coordinate 4 lies on the line segment joining the pointsP (2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.

[Hint suppose R divides PQ in the ratio k: 1. The coordinates of the point R are given by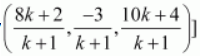

Solution :

The coordinates of points P and Q are given as P (2, –3, 4) and Q (8, 0, 10).

Let R divide line segment PQ in the ratio k:1.

Hence, by section formula, the coordinates of point R are given by

It is given that the x-coordinate of point R is 4.

Therefore, the coordinates of point R are

Question6. If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA² + PB² =k², wherek is a constant.

Solution :
The coordinates of points A and B are given as (3, 4, 5) and (–1, 3, –7) respectively.

Let the coordinates of point P be (x, y, z).

On using distance formula, we obtain

Now, if PA² + PB² = k², then

Thus, the required equation is<