NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Miscellaneous Exercise

NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Miscellaneous Exercise

NCERT Solutions for Class-11 Maths Chapter-8 Binomial Theorem

NCERT Solutions for Class-11 Maths Chapter-8 Binomial Theorem Miscellaneous Exercise prepared by the expert of Physics Wallah score more with Physics Wallah NCERT Class-11 maths solutions. You can download NCERT solutions of all chapters from Physics Wallah NCERT solutions of class 11.

NCERT Solutions for Class-11 Maths Miscellaneous Exercise

Question 1. Find a, b and n in the expansion of (a + b) ⁿ if the first three terms of the expansion are 729, 7290 and 30375, respectively.

Solution :
Given: (a + b) ⁿ

T _r+1 = ⁿ C _r a ^n-t b ^r

The first three terms of the expansion are given as 729, 7290 and 30375 respectively. Then we have,

T1 = ⁿ C ₀ a ^n-0 b ⁰ = an = 729….. 1

T2 = ⁿ C ₁ a ^n-1 b ¹ = ⁿ a ^n-1 b = 7290…. 2

T3 = ⁿ C ₂ a ^n-2 b ² = {n (n -1)/2 }a ^n-2 b ² = 30375……3

Dividing 2 by 1 we get

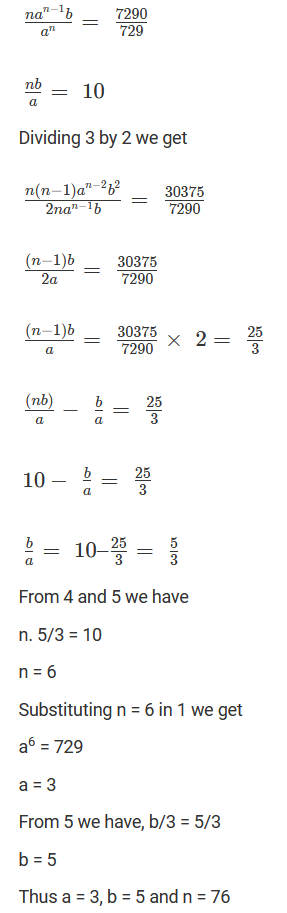
Question 2. Find a if the coefficients of x ² and x ³ in the expansion of (3 + ax) ⁹ are equal.

Solution :

Question 3. Find the coefficient of x ⁵ in the product (1 + 2x) ⁶ (1 – x) ⁷ using binomial theorem.

Solution :
Using Binomial Theorem,

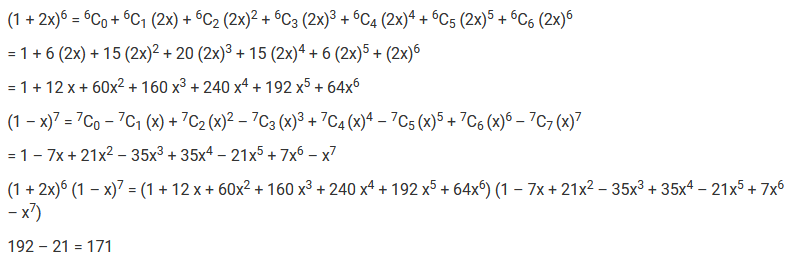
Question 4. If a and b are distinct integers, prove that a – b is a factor of a ⁿ – b ⁿ , whenever n is a positive integer.

[Hint: write an = (a – b + b) ⁿ and expand]

Solution :

n order to prove that (a – b) is a factor of (a ⁿ – b ⁿ ), it has to be proved that

a ⁿ – b ⁿ = k (a – b) where k is some natural number.

a can be written as a = a – b + b

an = (a – b + b) ⁿ = [(a – b) + b] ⁿ

= ⁿ C ₀ (a – b) ⁿ + ⁿ C ₁ (a – b) ^n-1 b + …… + ⁿ C _n b ⁿ

a ⁿ – b ⁿ = (a – b) [(a –b) ^n-1 + ⁿ C ₁ (a – b) ^n-1 b + …… + ⁿ C _n b ⁿ ]

a ⁿ – b ⁿ = (a – b) ^k

Where k = [(a –b) ^n-1 + ⁿ C ₁ (a – b) ^n-1 b + …… + ⁿ C _n b ^n] is a natural number

Question 5. Evaluate: (√3 + √2) ⁶ - (√3 - √2) ⁶

Solution :

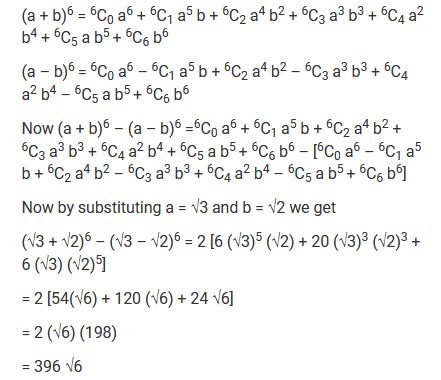
Question 6. Find the value of

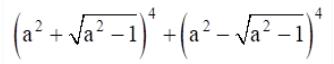
Solution :

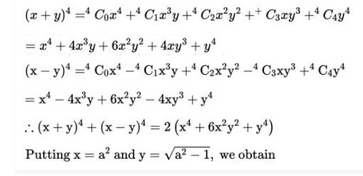
Question 7. Find an approximation of (0.99) ⁵ using the first three terms of its expansion.

Solution :
Here .99 can be written as

0.99 = 1 – 0.01

Now by applying binomial theorem we get

(o. 99)5 = (1 – 0.01) ⁵

= 5C0 (1) ⁵ – ⁵ C ₁ (1) ⁴ (0.01) + ⁵ C ₂ (1) ³ (0.01) ²

= 1 – 5 (0.01) + 10 (0.01) ²

= 1 – 0.05 + 0.001

= 0.951

Question 8. Find n if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 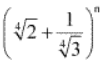is

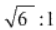
Solution :

Question 9. Expand using binomial theorem

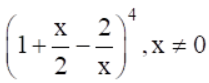
Solution :
We have

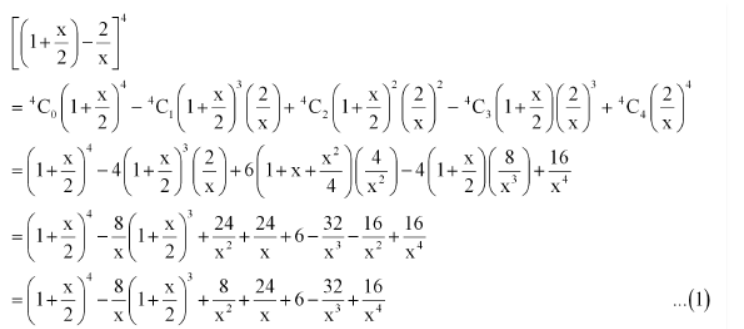
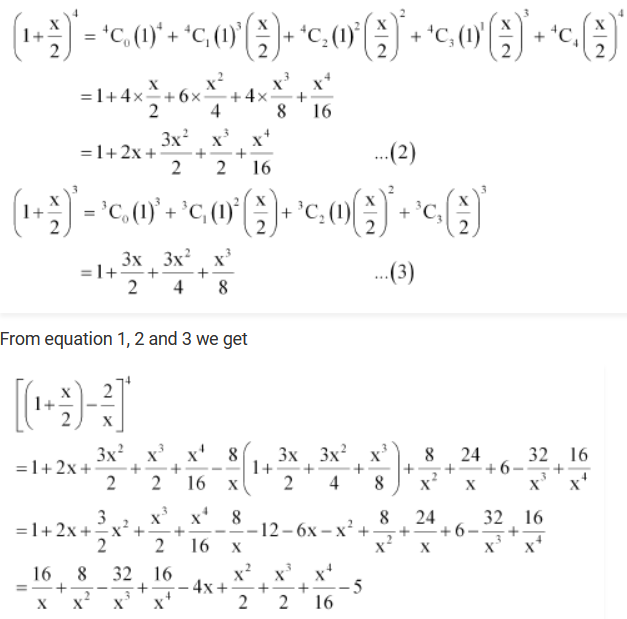
Question 10. Find the expansion of (3x ² – 2ax + 3a ² ) ³ using binomial theorem.

Solution :
Here

=  We know that (a + b) ³ = a ³ + 3a ² b + 3ab ² + b ³

Putting a = 3x ² & b = -a (2x-3a), we get
[3x ² + (-a (2x-3a))] ³

= (3x2) ³ +3(3x ² ) ² (-a (2x-3a)) + 3(3x ² ) (-a (2x-3a)) ² + (-a (2x-3a)) ³

= 27x ⁶ – 27ax ⁴ (2x-3a) + 9a2x ² (2x-3a) ² – a ³ (2x-3a) ³

= 27x ⁶ – 54ax ⁵ + 81a2x ⁴ + 9a2x ² (4x ² -12ax+9a ² ) – a3 [(2x)3 – (3a)3 – 3(2x) ² (3a) + 3(2x)(3a) ² ]

= 27x ⁶ – 54ax ⁵ + 81a ² x ⁴ + 36a ² x ⁴ – 108a ³ x ³ + 81a ⁴ x ² – 8a3x3 + 27a ⁶ + 36a ⁴ x2 – 54a ⁵ x

= 2 ^7x6 – 54ax ⁵ + 117a ² x ⁴ – 116a ³ x ³ + 117a ⁴ x ² – 54a ⁵ x + 27a ⁶

Thus, (3x ² – 2ax + 3a ² ) ³

= 27x ⁶ – 54ax ⁵ + 117a2x ⁴ – 116a ³ x ³ + 117a ⁴ x ² – 54a ⁵ x + 27a ⁶