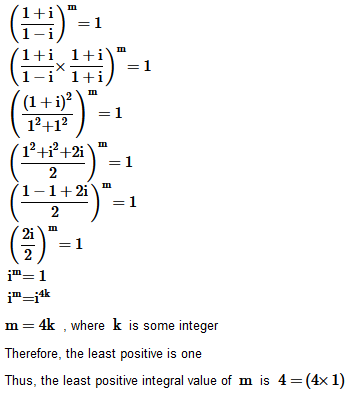chapter-5 Complex Number And Quadratic Equations Miscellaneous Exercise
NCERT Solutions for Class-11 Maths Chapter-5 Complex Number and Quadratic Equations
NCERT Solutions For Class-11 Maths
Chapter-5 Complex Number and Quadratic Equations Miscellaneous Exercise prepared by the expert of Physics Wallah score more with Physics Wallah NCERT Class-11 maths solutions. You can download solution of all chapters from Physics Wallah
NCERT solutions
of class 11.
NCERT Solutions for Class-11 Maths Chapter-5 Complex Number and Quadratic Equations Miscellaneous Exercise
Question
1. Evaluate:
[i
18
+ (1
/
i)
25
]
3
Solution :
Given: [i
18
+ (1
/
i)
25
]
3
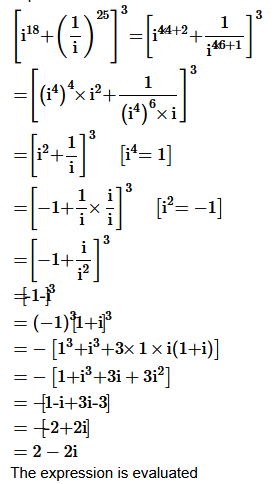
Question
2. For any two complex numbers z
1
and z
2
, prove that
Re (z
1
z
2
) = Re z
1
Re z
2
– Im z
1
Im z
2
Solution :
Let z
1
= x
1
+ iy
1
and z
2
= x
2
+ iy
2
∴z
1
z
2
= (x
1
+iy
1
) (x
2
+ iy
2
)
=x1(x
2
+ iy
2
) + iy
1
(x
2
+ ty
2
)
=x
1
x
2
+ ix
1
y
2
+ iy
1
x
2
+ i2y
1
y
2
=x
1
x
2
+ ix
1
y
2
+ iy
1
x
2
− y
1
y
2
=(x
1
x
2
− y
1
y
2
) + i(x
2
y
2
+ y
1
x
2
)
⇒Re(z
1
z
2
)= x
1
x
2
− y
1
y
2
⇒Re (z
1
z
2
) = Rez
1
Rez
2
− lmz
1
Imz
2
Hence, proved.
Question
3. Reduce
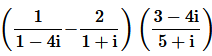 to the standard form.
to the standard form.
Solution :

Question
4. If
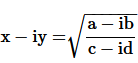 prove that
prove that
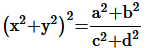
Solution :

Question
5. Convert the following in the polar form:
(i)
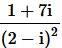
(ii)
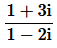
Solution :

This is the required polar form.
(ii) Here
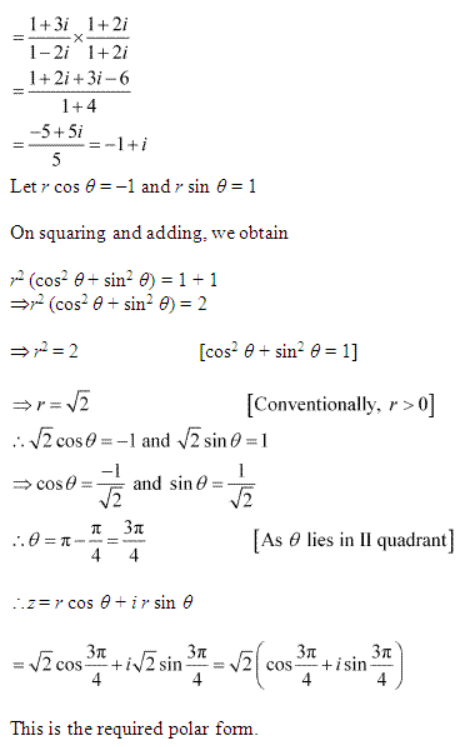
Solve each of the equations in exercises 6 to 9:
Question
6.
3x
2
-4x + 20/3 = 0
Solution :

Question
7.
x
2
-2x + 3/2 = 0
Solution
. Given:

Question
8. Solve the equation 27x
2
– 10x + 1 = 0
Solution :
Given:

Question
9. Solve the equation 21x
2
– 28x + 10 = 0
Solution :
Given:
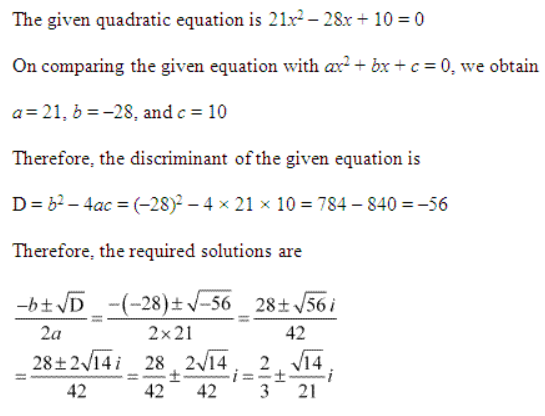
Question
10. If
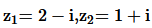 find
find
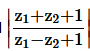
Solution :
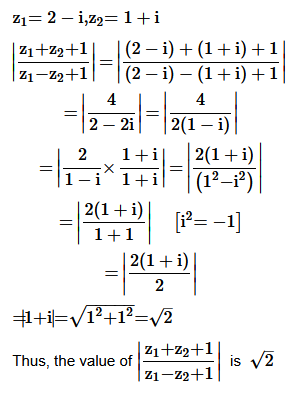
Question
11. If
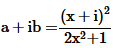 prove that
prove that
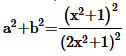
Solution :
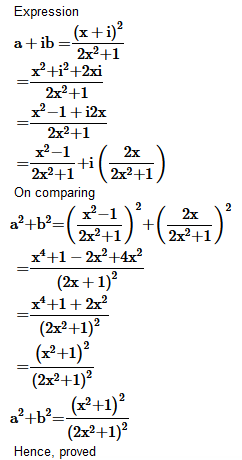
Question
12. Let z
1
=2−i,z
2
=−2+i. Find
(i) Re (z
1
z
2
/z
1
),
(ii) Im (1z
1
/ z
1
)
Solution :

Question
13. Find the modulus and argument of the complex number
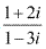
Solution :

Question
14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i.
Solution :
Let = (x−ty) (3+5i)z
=3x + 5xi − 3yi − 5yi
2
=3x + 5xi − 3yi + 5y
=(3x+5y) + i(5x−3y)
∴z =(3x+5y) −i (5x−3y)
It is given that,z=−6−24i
∴(3x+5y) −i(5x−3y) =−6−24i
Equating real and imaginary parts, we obtain
3x+5y=−6
5x−3y=24
Multiplying equation (i) by 3 and equation (ii) by 5 and then adding them, we obtain
Putting the value ofxin equation (i),
we obtain 3(3)+ 5y=−6⇒ 5y=−6−15 ⇒y=−3
Thus, the values of x and y are 3 and − 3 respectlvely.
Question
15. Find the modulus of
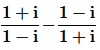
Solution :
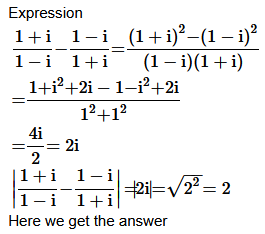
Question
16. If
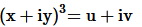 then show that
then show that
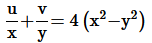
Ans. Given:
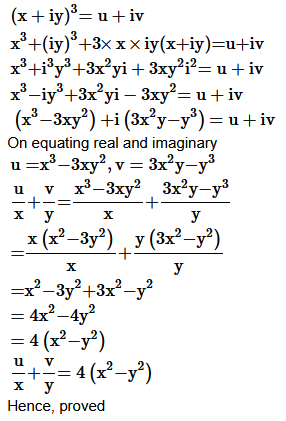
Question
17. If α and β are different complex numbers with | β | = 1 then find
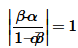
Solution :
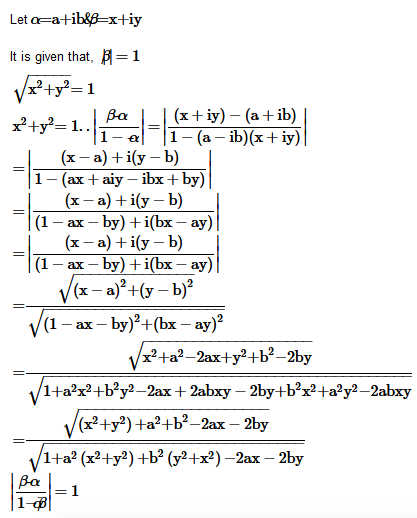
Question
18. Find the number of non-zero integral solutions of the equation
|
1−i|
x
=
2
x
Solution :
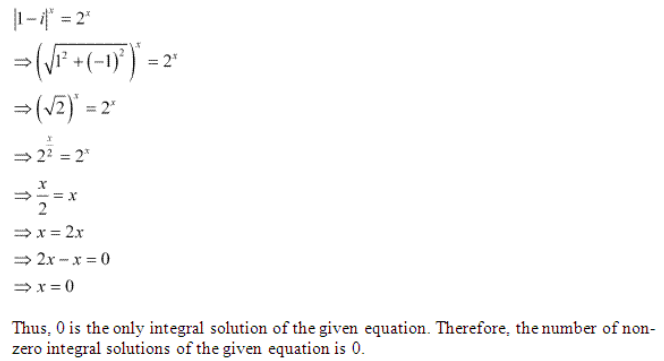
Question
19. If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that
(a
2
+ b
2
) (c
2
+ d
2
) (e
2
+ f
2
) (g
2
+ h
2
) = A
2
+ B
2
.
Solution :
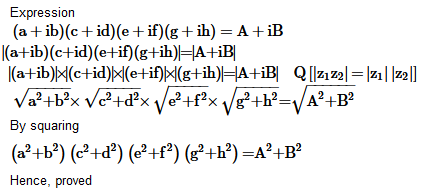
Question
20. If
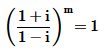 then find the least positive integral value of m.
then find the least positive integral value of m.
Solution :