NCERT Solutions For Class 11 Maths chapter-11 Conic Sections Exercise 11.4

NCERT Solutions For Class 11 Maths chapter-11 Conic Sections Exercise 11.4

NCERT Solutions for Class-11 Maths Chapter-11 Conic Sections

NCERT Solutions for Class 11 Maths Chapter-11 Conic Sections Exercise 11.4 is prepared by expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download and share NCERT Solutions for Class 11 Maths.

NCERT Solutions for Class-11 Maths Exercise 11.4

In each of the Exercises 1 to 6, find the coordinates of the foci, and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.

Question 1.

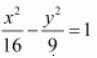
Solution :

The given equation is .

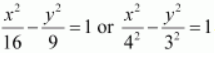On comparing this equation with the standard equation of hyperbola i.e., 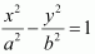, we obtain a = 4 and b = 3.

We know that a ² + b ² = c ² .

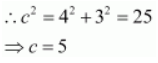
Therefore,

The coordinates of the foci are (±5, 0).

The coordinates of the vertices are (±4, 0).

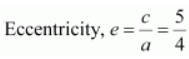
Length of latus rectum

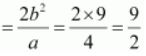
Question 2.

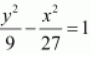
Solution :

The given equation is .

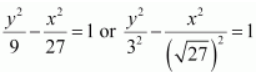On comparing this equation with the standard equation of hyperbola i.e., 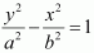, we obtain a = 3 and .

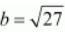We know that a ² + b ² = c ² .

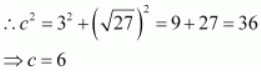
Therefore,

The coordinates of the foci are (0, ±6).

The coordinates of the vertices are (0, ±3).

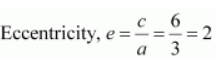
Length of latus rectum

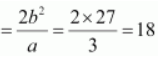
Question 3.9 y ² −4x ² = 36

Solution :

The given equation is 9 y ² – 4 x ² = 36.

It can be written as

9 y ² – 4 x ² = 36

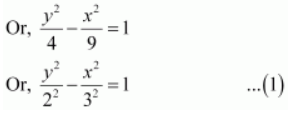
On comparing equation (1) with the standard equation of hyperbola i.e., 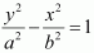, we obtain a = 2 and b = 3.

We know that a ² + b ² = c ² .

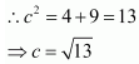
Therefore,

The coordinates of the foci are .

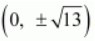The coordinates of the vertices are .

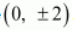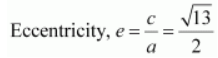
Length of latus rectum

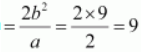
Question 4. Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola 16x ² – 9y ² = 576

Solution :

The given equation is 16 x ² – 9 y ² = 576.

It can be written as

16 x ² – 9 y ² = 576

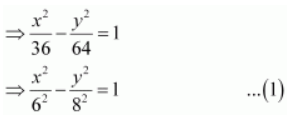
On comparing equation (1) with the standard equation of hyperbola i.e., 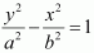, we obtain a = 6 and b = 8.

We know that a ² + b ² = c ² .

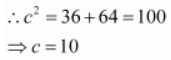
Therefore,

The coordinates of the foci are (±10, 0).

The coordinates of the vertices are (±6, 0).

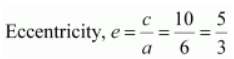
Length of latus rectum

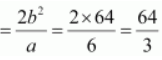
Question 5.5 y ² – 9x ² = 36

Solution :

The given equation is 5 y ² – 9 x ² = 36.

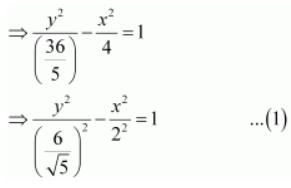
On comparing equation (1) with the standard equation of hyperbola i.e., 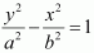, we obtain a = 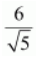and b = 2.

We know that a ² + b ² = c ² .

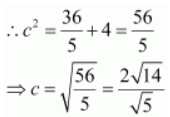
Therefore, the coordinates of the foci are .

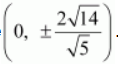The coordinates of the vertices are .

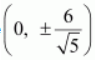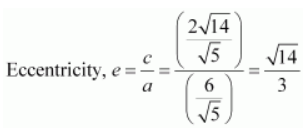
Length of latus rectum

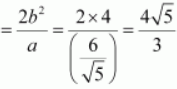
Question 6. 49 x ² = 784

Solution :

The given equation is 49 y ² – 16 x ² = 784.

It can be written as
49 y ² – 16 x ² = 784

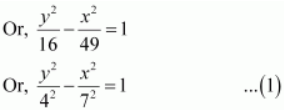
On comparing equation (1) with the standard equation of hyperbola i.e., 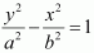, we obtain a = 4 and b = 7.

We know that a ² + b ² = c ² .

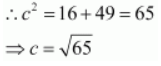
Therefore,

The coordinates of the foci are .

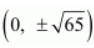The coordinates of the vertices are (0, ±4).

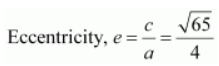
Length of latus rectum

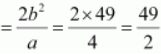
In each of the Exercises 7 to 15, find the equation of the hyperbola satisfying the given conditions.

Question 7. Find the equation of the hyperbola satisfying the give conditions: Vertices (±2, 0), foci (±3, 0)

Solution :

Vertices (±2, 0), foci (±3, 0)

Here, the vertices are on the x -axis.

Therefore, the equation of the hyperbola is of the form .

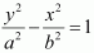Since the vertices are (±2, 0), a = 2.

Since the foci are (±3, 0), c = 3.

We know that a ² + b ² = c ² .

so, 2 ² + b ² = 3 ²

b ² = 9 - 4 = 5

Thus, the equation of the hyperbola is .

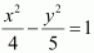Question 8. Find the equation of the hyperbola satisfying the give conditions: Vertices (0, ±5), foci (0, ±8)

Solution :

Vertices (0, ±5), foci (0, ±8)

Here, the vertices are on the y -axis.

Therefore, the equation of the hyperbola is of the form .

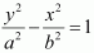Since the vertices are (0, ±5), a = 5.

Since the foci are (0, ±8), c = 8.

We know that a ² + b ² = c ² .

so, 5 ² + b ² = 8 ²

b ² = 64 - 25 = 39

Thus, the equation of the hyperbola is

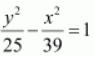
Question 9. Find the equation of the hyperbola satisfying the give conditions: Vertices (0, ±3), foci (0, ±5)

Solution :

Vertices (0, ±3), foci (0, ±5)

Here, the vertices are on the y -axis.

Therefore, the equation of the hyperbola is of the form .

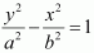Since the vertices are (0, ±3), a = 3.

Since the foci are (0, ±5), c = 5.

We know that a ² + b ² = c ² .

∴3 ² + b ² = 5 ²

⇒ b ² = 25 – 9 = 16

Thus, the equation of the hyperbola is .

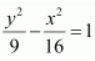Question 10. Foci (±5, 0), the transverse axis is of length 8.

Solution :
Given:

Foci (±5, 0), the transverse axis is of length 8.

Here, the foci are on the x -axis.

Therefore, the equation of the hyperbola is of the form .

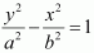Since the foci are (±5, 0), c = 5.

Since the length of the transverse axis is 8, 2 a = 8 ⇒ a = 4.

We know that a ² + b ² = c ² .

∴4 ² + b ² = 5 ²

⇒ b ² = 25 – 16 = 9

Thus, the equation of the hyperbola is .

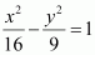Question 11. Foci (0, ±13), the conjugate axis is of length 24.

Solution :
Given:

Foci (0, ±13), the conjugate axis is of length 24.

Here, the foci are on the y -axis.

Therefore, the equation of the hyperbola is of the form .

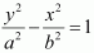Since the foci are (0, ±13), c = 13.

Since the length of the conjugate axis is 24, 2 b = 24 ⇒ b = 12.

We know that a ² + b ² = c ² .

∴ a ² + 12 ² = 13 ²

⇒ a ² = 169 – 144 = 25

Thus, the equation of the hyperbola is .

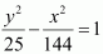Question 12. Foci 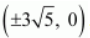the latus rectum is of length 8.

Solution :

Foci 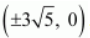, the latus rectum is of length 8.

Here, the foci are on the x -axis.

Therefore, the equation of the hyperbola is of the form .

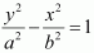Since the foci are 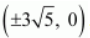, c = .

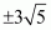Length of latus rectum = 8

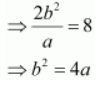
We know that a ² + b ² = c ² .

∴ a ² + 4 a = 45

⇒ a ² + 4 a – 45 = 0

⇒ a ² + 9 a – 5 a – 45 = 0

⇒ ( a + 9) ( a – 5) = 0

⇒ a = –9, 5

Since a is non-negative, a = 5.

∴ b ² = 4 a = 4 × 5 = 20

Thus, the equation of the hyperbola is

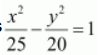
Question 13. Foci (±4, 0), the latus rectum is of length 12

Solution :

Foci (±4, 0), the latus rectum is of length 12.

Here, the foci are on the x -axis.

Therefore, the equation of the hyperbola is of the form .

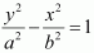Since the foci are (±4, 0), c = 4.

Length of latus rectum = 12

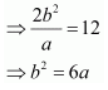
We know that a ² + b ² = c ² .

∴ a ² + 6 a = 16

⇒ a ² + 6 a – 16 = 0

⇒ a ² + 8 a – 2 a – 16 = 0

⇒ ( a + 8) ( a – 2) = 0

⇒ a = –8, 2

Since a is non-negative, a = 2.

∴ b ² = 6 a = 6 × 2 = 12

Thus, the equation of the hyperbola is .

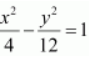Question 14. Vertices (±7, 0),e = 4/3

Solution :

Vertices (±7, 0), e = 4/3

Here, the vertices are on the x -axis.

Therefore, the equation of the hyperbola is of the form .

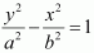Since the vertices are (±7, 0), a = 7.

It is given that e = 4/3

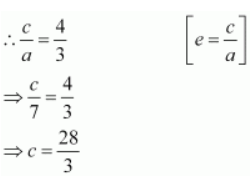
We know that a ² + b ² = c ² .

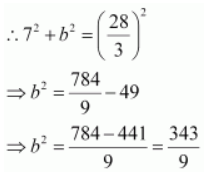
Thus, the equation of the hyperbola is

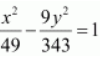
Question 15. Foci (0,±√10), passing through (2,3)

Solution :

Foci(0,±√10), passing through (2, 3)

Here, the foci are on the y -axis.

Therefore, the equation of the hyperbola is of the form .

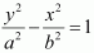Since the foci are(0,±√10), c =√10.

We know that a ² + b ² = c ² .

∴ a ² + b ² = 10

⇒ b ² = 10 – a ² … (1)

Since the hyperbola passes through point (2, 3),

From equations (1) and (2), we obtain

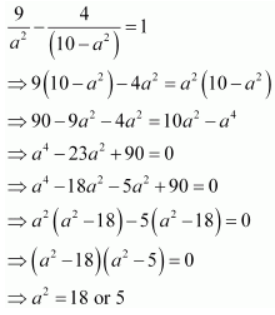
In hyperbola, c > a , i.e., c ² > a ²

∴ a ² = 5

⇒ b ² = 10 – a ² = 10 – 5 = 5

Thus, the equation of the hyperbola is .
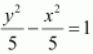