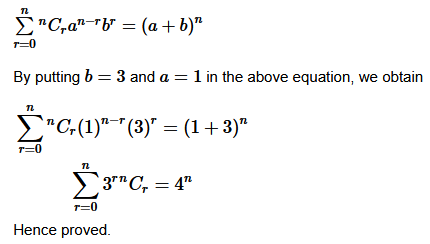NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Exercise 8.1

NCERT Solutions For Class 11 Maths chapter-8 Binomial Theorem Exercise 8.1

NCERT Solutions for Class-11 Maths Chapter-8 Binomial Theorem

NCERT Solutions For Class 11 Maths Chapter-8 Binomial Theorem Exercise 8.1 prepared by the expert of Physics Wallah score more with Physics Wallah NCERT Class 11 maths solutions. You can download solution of all chapters from Physics Wallah NCERT solutions of class 11.

NCERT Solutions for Class-11 Maths Exercise 8.1

Expand each of the expression in Exercises 1 to 5.

Question 1. Expand the expression (1– 2x) ⁵

Solution :
Using Binomial Theorem,

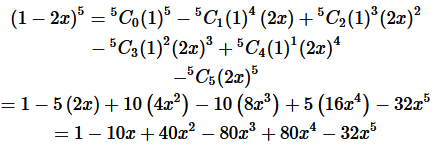
Question 2.

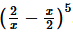
Solution :
Using Binomial Theorem,

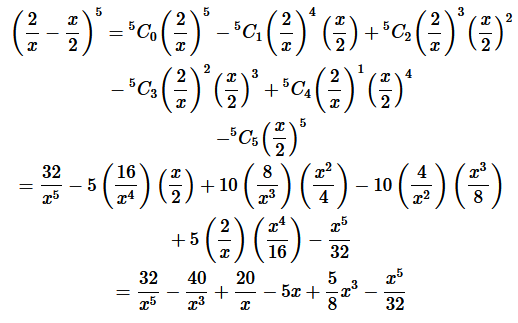
Question 3. Expand the expression (2x – 3) ⁶

Solution :
Using Binomial Theorem,

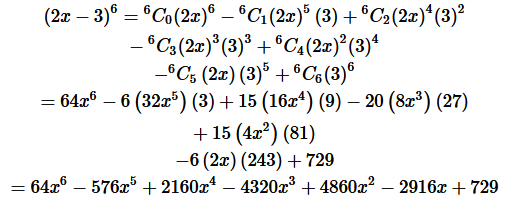
Question 4.

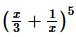
Solution :
Using Binomial Theorem,

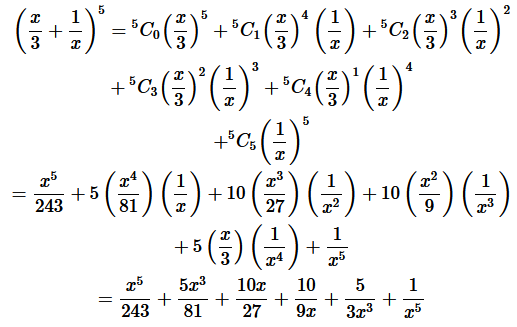
Question 5.

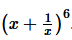
Solution :
Using Binomial Theorem,

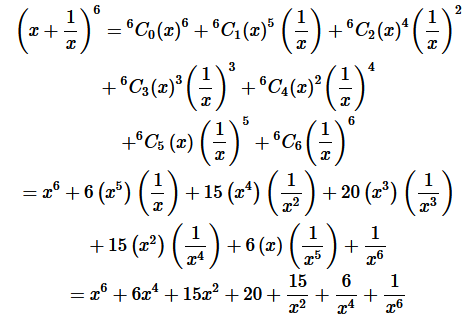
Using binomial theorem evaluate each of the following:

Question 6. Using Binomial Theorem, evaluate (96) ³

Solution :
Given: 96 ³

^{96 = 100 - 4}

Using Binomial Theorem,

(96) ³ = (100−4) ³ = ³ C ₀ (100) ³ − ³ C ₁ (100) ² (4) + ³ C ₂ (100)(4) ² − ³ C ₃ (4) ³

=1000000−3(10000)(4)+3(100)(16)−64

=1000000−120000+4800−64

=884736

Question 7 .Using Binomial Theorem, evaluate (102) ⁵

Solution :
Given: (102) ⁵

Using Binomial Theorem,

= (102) ⁵ = (100+2) ⁵ = ⁵ C ₀ (100) ⁵ + ⁵ C ₁ (100) ⁴ (2) + ⁵ C ₂ (100) ³ (2) ² + ⁵ C ₃ (100) ² (2) ³ + ⁵ C ₄ (100)(2) ⁴ + ⁵ C ₅ (2) ⁵

=10000000000+5(100000000)(2)+10(1000000)(4)+10(10000)(8)+5(100)(16)+32

= 10000000000 + 1000000000 + 40000000 + 800000 + 8000 + 32

= 11040808032

Question 8. Using Binomial Theorem, evaluate (101) ⁴

Solution :
Given: (101) ⁴

Using Binomial Theorem,

101 = 100+1



(101) ⁴ =(100+1) ⁴

= ⁴ C ₀ (100) ⁴ + ⁴ C ₁ (100) ³ (1)+ ⁴ C ₂ (100) ² (1) ² + ⁴ C _{^{3 (}} 100)(1) ³ + ⁴ C ₄ (1) ⁴

=100000000+4(1000000)+6(10000)+4(100)+1

= 100000000 + 4000000 + 60000 + 400 + 1

= 104060401

9. Using Binomial Theorem, evaluate (99) ⁵

Solution :
Given: (99) ⁵

Using Binomial Theorem,

(99) ⁵ =(100−1) ⁵

= ⁵ C ₀ (100) ⁵ − ⁵ C ₁ (100) ⁴ (1)+ ⁵ C ₂ (100) ³ (1) ² − ⁵ C ₃ (100) ² (1) ³ + ⁵ C ₄ (100)(1) ⁴ − ⁵ C ₅ (1) ⁵

=10000000000−5(100000000)−10(1000000)−10(10000)+5(100)−1=

= 10000000000 – 500000000 + 10000000 – 100000 + 500 – 1

= 9509900499

Question 10. Using Binomial Theorem, indicate which number is larger (1.1) ¹⁰⁰⁰⁰ or 1000.

Solution :
Given: (1.1) ¹⁰⁰⁰⁰ or 1000.

Using Binomial Theorem,

By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)10000

be obtained as

(1.1) ¹⁰⁰⁰⁰ =(1+0.1) ¹⁰⁰⁰⁰

= ¹⁰⁰⁰⁰ C ₀ + ¹⁰⁰⁰⁰ C ₁ (1.1) + Other positive terms

=1+10000×1.1+Other positive terms

=1+11000+Other positive terms>1000

Hence, (1.1)10000>1000

Question 11. Find (a + b) ⁴ – (a – b) ⁴ . Hence, evaluate (√3 + √2) ⁴ - (√3 - √2) ^4.

Solution :
Given: (a + b) ⁴ – (a – b) ⁴

Using Binomial Theorem,

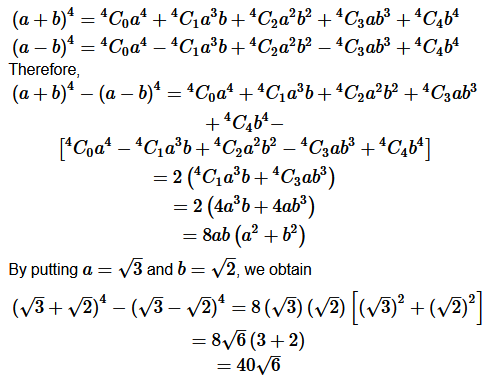
Question 12. Find (x + 1) ⁴ – (x – 1) ⁴ Hence or otherwise evaluate (√ 2 + 1 ) ⁶ + (6 -1 ) ⁶

Solution :
Given: (x + 1) ⁴ – (x – 1) ⁴

Using Binomial Theorem,

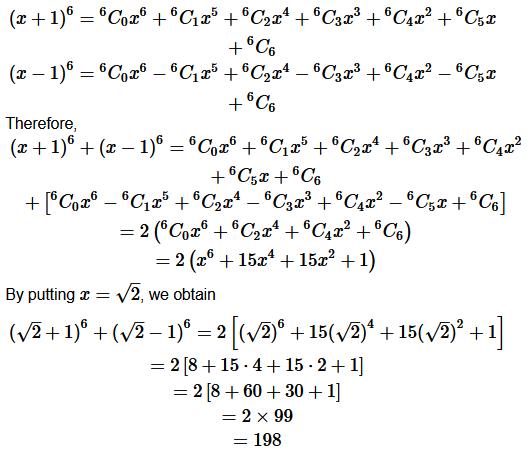
Question 13. Show that 9 ⁿ⁺¹ is divisible by 64 whenever n is a positive integer.

Solution :
Given:   9 ⁿ⁺¹ is divisible by 64

In order to show that 9 ⁿ⁺¹ −8n−9 is divisible by 64, it has to be prove that, 9 ⁿ⁺¹ −8n−9=64k

, where k is some natural number.

Using Binomial Theorem,

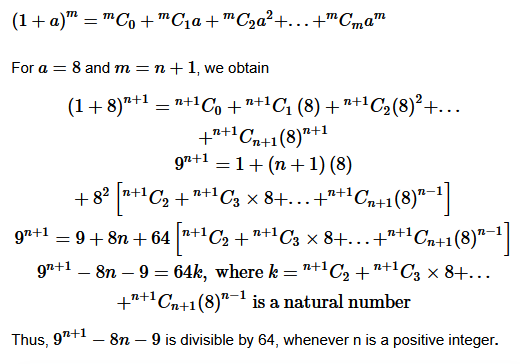
Question 14. Prove that

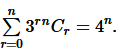
Solution :