Angle Of Depression

question 1. Find the angle of elevation of the Sun's altitude when the height of shadow of a vertical pole is equal to its height.

Solution: Let the height of the pole AB = x m.

Then length of shadow OB of the pole AB = x m.

[ height of shadow = height of pole]

Let the angle of elevation be θ, i.e. ∠AOB = θ

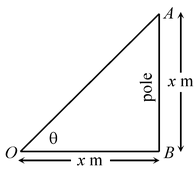
In right ΔOBA, we have

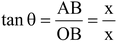⇒ tan θ = 1 ⇒ θ = 45º

Hence, the angle of elevation of the Sun's altitude is 45º.

question 2. In figure, what are the angle of depression of the top and bottom of h m tall building from the top of multistoried building?

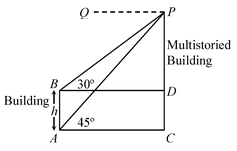
Solution: From P draw a line PQ || BD or AC, then the angles of depression of the top and bottom of a tall building h m from the top P of the multistoried building are 30º and 45º, respectively.

question 3. From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. Find the height of the tower.

Solution: Let O be a point 20 m away from the tower AB = h m. In right ΔOBA, we have

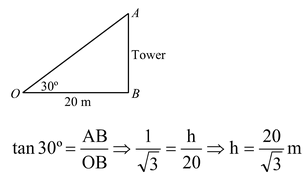
Thus, the height of the tower is 20/√3 m.

question 4. In figure, what are the angles of depression of the top and bottom of a pole from the top of a tower h m high?

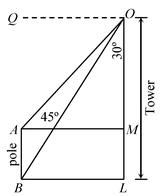
Solution: From O draw a line OQ parallel to AM or BL, then the angles of depression of the top and bottom of a pole from the top O of a tower h m are 45º and 60º respectively.

question 5. A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevations of the top of a hill as 60o and the angle of depression of the base of the hill as 30o. Calculate the distance of the hill from the ship and the height of the hill.

Solution: Let x be distance of hill from man and h + 8 be height of hill which is required.

ΔABC is right triangle ∠ACB.

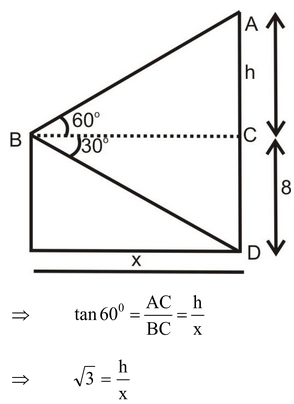
In right triangle BCD,

Height of hill = h + 8 = 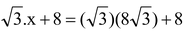= 32m.

Distance of ship from hill = x = 8√3 m.