Progressions

Those sequence whose terms follow certain patterns are called progression. Generally there are three types of progression.

• Arithmetic Progression (A.P.)
• Geometric Progression (G.P.)
• Harmonic Progression (H.P.)

ARITHMETIC PROGRESSION:

A sequence is called an A.P., if the difference of a term and the previous term is always same. i.e. d = t_n+1 – t_n = Constant for all n ∊ N. The constant difference, generally denoted by ‘d’ is called the common difference.

question 1. Find the common difference of the following A.P. : 1,4,7,10,13,16 ......

Solution: 4 – 1 = 7 – 4 = 10 – 7 = 13 – 10 = 16 – 13 = 3 (constant).

∴ Common difference (d) = 3.

GENERAL FORM OF AN A.P. :

If we denote the starting number i.e. the 1st number by ‘a’ and a fixed number to the added is ‘d’ then a, a + d, a + 2d, a + 3d, a + 4d, ...... forms an A.P.

question 1. Find the A.P. whose 1st term is 10 & common difference is 5.

Solution: Given : First term (a) = 10 & Common difference (d) = 5.

∴ A.P. is 10, 15, 20, 25, 30. ...

nth TERM OF AN A.P. :

Let A.P. be a, a + d, a + 2d, a + 3d. ...

Then, First term (a₁) = a + 0.d

Second term (a₂) = a + 1.d

Third term (a₃) = a + 2.d

n^th term (a_n) = a + (n - 1) d

∴ an = a + (n - 1) d is called the nth term.

question 1. Determine the A.P. whose third term is 16 and the difference of 5th term from 7th term is 12.

Solution: Given: a³ = a + (3 – 1) d = a + 2d = 16 .....(i)

a⁷ – a⁵ = 12 ....(ii)

(a + 6d) – (a + 4d) = 12

a + 6d – a – 4d = 12

2d = 12

d = 6

Put d = 6 in equation (i)

a = 16 - 12

a = 4

∴ A.P. is 4, 10, 16, 22, 28, ......

2. Which term of the sequence 72, 70, 68, 66, ..... is 40 ?

Solution: Here 1st term x = 72 and common difference d = 70 – 72 = –2

∴ For finding the value of n

an = a + (n – 1)d

⇒ 40 = 72 + (n – 1) (–2)

⇒ 40 – 72 = –2_{n + 2}

⇒ –32 = –2_{n + 2}

⇒ –34 = –2_n

⇒ n = 17

⇒ 17^th term is 40.

TO FIND nth TERM FROM THE END OF AN A.P.:

Consider the following A.P. a, a + d, a + 2d, … (l – 2d), (l – d), l

where l is the last term

last term l = l − (1 − 1)d

2^nd last term l − d = l − (2 − 1) d

3^rd last term l − 2d = l − (3 − 1)d

n^th term from the end = l − (n − 1) d

question 1. Find the 5^th term from the end of the AP, 17, 14, 11, ….., −40

Solution: 1st method

l = -40, d = 14 - 17 = -3

Using l − (n − 1) d

5^th term from the end will be

= -40 - (5 - 1) x -3

= -40 - 40 x -3

= -40 + 12

= −28

2^nd method

Sequence can be written as −40, −37, ….11, 14, 17

∴ a = -40

d = -37 - ( - 40)

= −37 + 40

= 3

n = 5

Using an = a + (n - 1)d

=-40 + (5 - 1) x -3

= -40 + 4 x -3

= −40 + 12

= −28

SELECTION OF TERMS IN AN A.P. :

Sometimes we require certain number of terms in A.P. The following ways of selecting terms are generally very convenient.

question 1. The sum of three number in A.P. is -3 and their product is 8. Find the numbers.

Solution: Three no. ‘s in A.P. be a – d, a, a + d

∴ a – d + a + a + d = – 3

3a = –3 ⇒ a = –1

& (a – d) a (a + d) = 8

a(a₂ – d₂) = 8

(–1) (1 – d₂) = 8

1 – d₂ = –8

⇒ d₂ = 9

⇒ d = ±  3

If a = 8 & d = 3 numbers are –4, –1, 2.

If a = 8 & d = – numbers are 2, –1, –4.

SUM OF n TERMS OF AN A.P. :

Let A.P. be a, a + d, a + 2d, a + 3d,...... a + (n - 1)d

Then,Sn = a + (a + d) + ..... + {a + (n - 2) d} + {a + (n - 1) d} .....(i)

also, Sn = {a + (n - 1)d} + {a + (n - 2)d} + ...... + (a + d) + a .....(ii)

Add (i) & (ii)

⇒ 2Sn = 2a + (n – 1)d + 2a + (n – 1)d + ............. + 2a + (n – 1)d

⇒ 2Sn = n [2a + (n – 1)d]

⇒ .

question 1. Find the sum of 20 terms of the A.P. 1, 4, 7, 10...

Solution: a = 1, d = 3

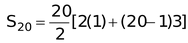
question 2. Find the sum of all three digit natural numbers. Which are divisible by 7.

Solution: 1^st no. is 105 and last no. is 994.

We can find n as

 994 = 105 + (n + 1)7

∴ n = 128

∴ Sum,  S₁₂₈ = 128[105 + 994]

PROPERTIES OF A.P. :

(A) For any real numbers a and b, the sequence whose nth term is an = an + b is always an A.P. with common difference ‘a’ (i.e. coefficient of term containing n)

(B) If any nth term of sequence is a linear expression in n then the given sequence is an A.P.

(C) If a constant term is added to or subtracted from each term of an A.P. then the resulting sequence is also an A.P. with the same common difference.

(D) If each term of a given A.P. is multiplied or divided by a non-zero constant K, then the resulting sequence is also an A.P. with common difference Kd or K/d respectively. Where d is the common difference of the given A.P.

(E) In a finite A.P. the sum of the terms equidistant from the beginning and end is always same and is equal to the sum of 1st and last term.

(F) If three numbers a, b, c are in A.P., then 2b = a + c.

question 1. Check whether an = 2_n2 + 1 is an A. P. or not.

Solution: an = 2_{n2 + 1}

Then an+1 = 2 (n + 1)² + 1

∴ a_n+1 – an = 2(n₂ + 2_{n + 1}) + 1 – 2_{n2 – 1}

= 2_n2 + 4_{n + 2} + 1 - 2_{n2 – 1}

= 4n + 2, which is not constant

∴ The above sequence is not an A.P.