
NCERT Solutions for Class 12 Maths Chapter 13
NCERT Solutions for Class 12 Maths Chapter 13 : Students will find the solutions for Maths Class 12 Chapter 13 Probability here. These will be very helpful for their studies. What the chances are of an event occurring is referred to as probability. Students of Probability class 12 can learn the details of probability in details in this chapter. Repeated solving of the questions of Maths class 12 Chapter 13 Probability shall go a long way in helping students understand the method of problem solving. It’s very easy to understand the class 12 maths chapter 13 Probability solutions since experts in the subject at PhysicsWallah have picked the simplest method of providing the solutions. The NCERT Solutions for Class 12 Maths Chapter 13 Probability provided here adhere to the guidelines laid down in the latest CBSE syllabus for 2023-24. Available both online and as downloadable PDFs, students can easily avail the solutions for NCERT class 12 Maths Chapter 13 for free in the offline mode as well.NCERT Solutions for Class 12 Maths Chapter 13 Overview
All the important concepts linked with conditional probability are explained here. The solutions given here help form a clear understanding of the Baye’s Theorem, the independence of events and the multiplication rule of probability. Conditional probability measures the possibility of any event occurring under the observation that another even has occurred already in the field of probability theory. The solutions contained here are a detailed description of the core concepts contained in Chapter 13. They help students form a thorough understanding of probability principles and how they are applied.NCERT Solutions for Class 12 Maths Chapter 13 Probability
For easy understanding, Class 12 Maths Chapter 13 Probability solutions are given here in simple steps. Our experts have been mindful of the difficulties students face and hence, explained the problems in detail. Exercise 13.1 Page No: 538 1. Given that E and F are events, such that P (E) = 0.6, P (F) = 0.3 and P (E ∩ F) = 0.2, find P (E|F) and P (F|E). Solution: 2. Compute P (A|B), if P (B) = 0.5 and P (A ∩ B) = 0.32
Solution:
2. Compute P (A|B), if P (B) = 0.5 and P (A ∩ B) = 0.32
Solution:
 3. If P (A) = 0.8, P (B) = 0.5 and P (B|A) = 0.4, find
(i) P (A ∩ B)
(ii) P (A|B)
(iii) P (A
∪
B)
Solution:
3. If P (A) = 0.8, P (B) = 0.5 and P (B|A) = 0.4, find
(i) P (A ∩ B)
(ii) P (A|B)
(iii) P (A
∪
B)
Solution:

 4. Evaluate P (A
∪
B), if 2P (A) = P (B) = 5/13 and P (A|B) = 2/5.
Solution:
4. Evaluate P (A
∪
B), if 2P (A) = P (B) = 5/13 and P (A|B) = 2/5.
Solution:
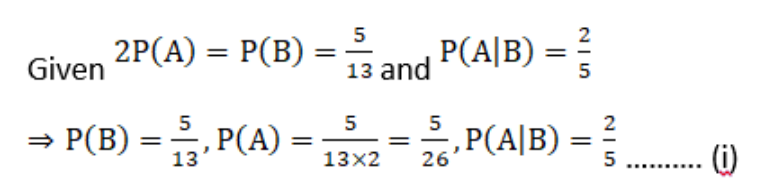
 5. If P (A) = 6/11, P (B) = 5/11 and P (A
∪
B) = 7/11, find
(i) P (A∩B)
(ii) P (A|B)
(iii) P (B|A)
Solution:
5. If P (A) = 6/11, P (B) = 5/11 and P (A
∪
B) = 7/11, find
(i) P (A∩B)
(ii) P (A|B)
(iii) P (B|A)
Solution:

 Determine P (E|F) in Exercises 6 to 9.
6. A coin is tossed three times, where
(i) E : head on the third toss, F : heads on first two tosses
(ii) E : at least two heads, F : at most two heads
(iii) E : at most two tails, F : at least one tail
Solution:
Determine P (E|F) in Exercises 6 to 9.
6. A coin is tossed three times, where
(i) E : head on the third toss, F : heads on first two tosses
(ii) E : at least two heads, F : at most two heads
(iii) E : at most two tails, F : at least one tail
Solution:


 (ii)
Here, E: no tail appears
And F: no head appears
⇒
E = {HH} and F = {TT}
⇒
E ∩ F = ϕ
(ii)
Here, E: no tail appears
And F: no head appears
⇒
E = {HH} and F = {TT}
⇒
E ∩ F = ϕ
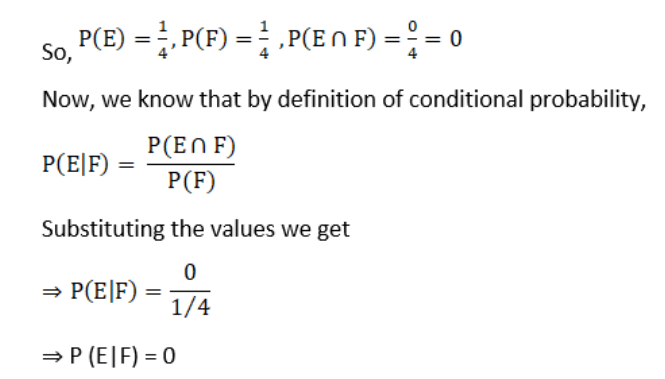 8. A die is thrown three times, E: 4 appears on the third toss, F: 6 and 5 appear, respectively, on the first two tosses.
Solution:
8. A die is thrown three times, E: 4 appears on the third toss, F: 6 and 5 appear, respectively, on the first two tosses.
Solution:
 9. Mother, father and son line up at random for a family picture
E: son on one end, F: father in the middle.
Solution:
Let M denotes mother, F denotes father, and S denotes son.
Then, the sample space for the given experiment will be
S = {MFS, SFM, FSM, MSF, SMF, FMS}
Here, E: Son on one end
And F: Father in the middle
⇒
E = {MFS, SFM, SMF, FMS} and F = {MFS, SFM}
⇒
E ∩ F = {MFS, SFM}
9. Mother, father and son line up at random for a family picture
E: son on one end, F: father in the middle.
Solution:
Let M denotes mother, F denotes father, and S denotes son.
Then, the sample space for the given experiment will be
S = {MFS, SFM, FSM, MSF, SMF, FMS}
Here, E: Son on one end
And F: Father in the middle
⇒
E = {MFS, SFM, SMF, FMS} and F = {MFS, SFM}
⇒
E ∩ F = {MFS, SFM}
 10. A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Solution:
10. A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Solution:


 11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5}
Find
(i) P (E|F) and P (F|E)
(ii) P (E|G) and P (G|E)
(iii) P ((E
∪
F)|G) and P ((E ∩ F)|G)
Solution:
11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5}
Find
(i) P (E|F) and P (F|E)
(ii) P (E|G) and P (G|E)
(iii) P ((E
∪
F)|G) and P ((E ∩ F)|G)
Solution:
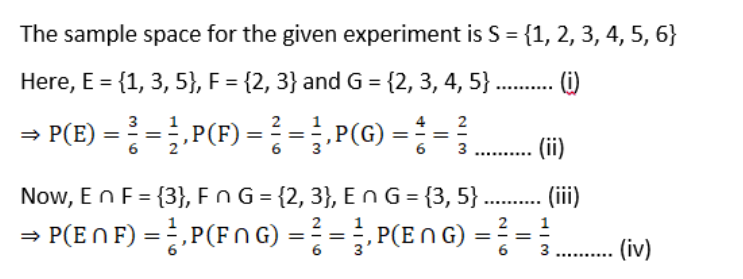


 12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?
Solution:
Let B denote boy and G denote girl.
Then, the sample space of the given experiment is S = {GG, GB, BG, BB}
Let E be the event that ‘both are girls’.
12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?
Solution:
Let B denote boy and G denote girl.
Then, the sample space of the given experiment is S = {GG, GB, BG, BB}
Let E be the event that ‘both are girls’.

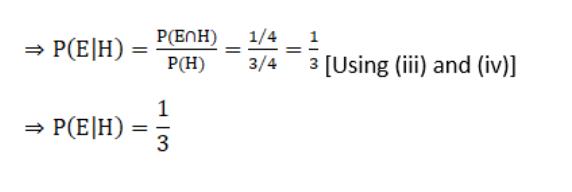 Exercise 13.2 Page No: 546
1. If P (A) = 3/5 and P (B) = 1/5, find P (A ∩ B) if A and B are independent events.
Solution:
Given P (A) = 3/5 and P (B) = 1/5
As A and B are independent events.
⇒
P (A ∩ B) = P (A).P (B)
= 3/5 × 1/5 = 3/25
2. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
Solution:
Given, a pack of 52 cards.
As we know, there are 26 cards in total, which are black. Let A and B denote, respectively, the events that the first and second drawn cards are black.
Now, P (A) = P (black card in first draw) = 26/52 = ½
Because the second card is drawn without replacement, now the total number of black cards will be 25, and the total number of cards will be 51, which is the conditional probability of B, given that A has already occurred.
Now, P (B/A) = P (black card in second draw) = 25/51
Thus, the probability that both cards are black
⇒
P (A ∩ B) = ½ × 25/51 = 25/102
Hence, the probability that both the cards are black = 25/102
3. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges, out of which 12 are good, and 3 are bad ones will be approved for sale.
Solution:
Given, a box of oranges.
Let A, B and C denotes the events, respectively, that the first, second and third drawn orange is good.
Now, P (A) = P (good orange in first draw) = 12/15
Because the second orange is drawn without replacement, now the total number of good oranges will be 11, and the total number of oranges will be 14, which is the conditional probability of B, given that A has already occurred.
Now, P (B/A) = P (good orange in second draw) = 11/14
Because the third orange is drawn without replacement, now the total number of good oranges will be 10, and the total oranges will be 13, which is the conditional probability of C, given that A and B have already occurred.
Now, P (C/AB) = P (good orange in third draw) = 10/13
Thus, the probability that all the oranges are good
⇒
P (A ∩ B ∩ C) = 12/15 × 11/14 × 10/13 = 44/91
Hence, the probability that a box will be approved for sale = 44/91
4. A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B are independent events or not.
Solution:
Given, a fair coin and an unbiased die are tossed.
We know that the sample space S.
S = {(H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
Let A be the event head that appears on the coin.
⇒
A = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}
⇒
P (A) = 6/12 = ½
Now, Let B be the event 3 on the die.
⇒
B = {(H, 3), (T, 3)}
⇒
P (B) = 2/12 = 1/6
As, A ∩ B = {(H, 3)}
⇒
P (A ∩ B) = 1/12 …… (1)
And P (A). P (B) = ½ × 1/6 = 1/12 …… (2)
From (1) and (2) P (A ∩ B) = P (A). P (B)
Therefore, A and B are independent events.
5. A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event, ‘the number is even’, and B be the event, ‘the number is red’. Are A and B independent?
Solution:
The sample space for the dice will be
S = {1, 2, 3, 4, 5, 6}
Let A be the event, and the number is even.
⇒
A = {2, 4, 6}
⇒
P (A) = 3/6 = ½
Now, let B be the event, and the number is red.
⇒
B = {1, 2, 3}
⇒
P (B) = 3/6 = 1/2
As, A ∩ B = {2}
⇒
P (A ∩ B) = 1/6 …….. (1)
And P (A). P (B) = ½ × ½ = ¼ ….. (2)
From (1) and (2) P (A ∩ B) ≠ P (A). P (B)
Therefore, A and B are not independent events.
6. Let E and F be events with P (E) = 3/5, P (F) = 3/10 and P (E ∩ F) = 1/5. Are E and F independent?
Solution:
Given P (E) = 3/5, P (F) = 3/10 and P (E ∩ F) = 1/5
P (E). P (F) = 3/5 × 3/10 = 9/50 ≠ 1/5
⇒
P (E ∩ F) ≠ P (E). P (F)
Therefore, E and F are not independent events.
7. Given that the events A and B are such that P (A) = 1/2, P (A
∪
B) = 3/5 and P (B) = p. Find p if they are (i) mutually exclusive (ii) independent.
Solution:
Given, P (A) = ½, P (A
∪
B) = 1/5 and P (B) = p
(i) Mutually exclusive
When A and B are mutually exclusive.
Then, (A ∩ B) = ϕ
⇒
P (A ∩ B) = 0
As we know, P (A
∪
B) = P (A) + P (B) – P (A ∩ B)
⇒
3/5 = ½ + p -0
⇒
P = 3/5 – ½ = 1/10
(ii)
Independent
When A and B are independent.
⇒
P (A ∩ B) = P (A). P (B)
⇒
P (A ∩ B) = ½ p
As we know, P (A
∪
B) = P (A) + P (B) – P (A ∩ B)
⇒
3/5 = ½ + 2 – p/2
⇒
p/2 = 3/5 – ½
⇒
p = 2 × 1/10 = 1/5
8. If A and B are two events such that P (A) = 1/4 , P (B) = 1/2 and P (A ∩ B) = 1/8, find P (not A and not B).
Solution:
Given P (A) = ¼, P (B) = ½ and P (A ∩ B) = 1/8
P (not A and not B) = P (A
’
∩ B
’
)
As, { A
’
∩ B
’
= (A
∪
B)
’
}
⇒
P (not A and not B) = P ((A
∪
B)
’
)
= 1 – P (A
∪
B)
= 1- [P (A) + P (B) – P (A ∩ B)]
Exercise 13.2 Page No: 546
1. If P (A) = 3/5 and P (B) = 1/5, find P (A ∩ B) if A and B are independent events.
Solution:
Given P (A) = 3/5 and P (B) = 1/5
As A and B are independent events.
⇒
P (A ∩ B) = P (A).P (B)
= 3/5 × 1/5 = 3/25
2. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.
Solution:
Given, a pack of 52 cards.
As we know, there are 26 cards in total, which are black. Let A and B denote, respectively, the events that the first and second drawn cards are black.
Now, P (A) = P (black card in first draw) = 26/52 = ½
Because the second card is drawn without replacement, now the total number of black cards will be 25, and the total number of cards will be 51, which is the conditional probability of B, given that A has already occurred.
Now, P (B/A) = P (black card in second draw) = 25/51
Thus, the probability that both cards are black
⇒
P (A ∩ B) = ½ × 25/51 = 25/102
Hence, the probability that both the cards are black = 25/102
3. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges, out of which 12 are good, and 3 are bad ones will be approved for sale.
Solution:
Given, a box of oranges.
Let A, B and C denotes the events, respectively, that the first, second and third drawn orange is good.
Now, P (A) = P (good orange in first draw) = 12/15
Because the second orange is drawn without replacement, now the total number of good oranges will be 11, and the total number of oranges will be 14, which is the conditional probability of B, given that A has already occurred.
Now, P (B/A) = P (good orange in second draw) = 11/14
Because the third orange is drawn without replacement, now the total number of good oranges will be 10, and the total oranges will be 13, which is the conditional probability of C, given that A and B have already occurred.
Now, P (C/AB) = P (good orange in third draw) = 10/13
Thus, the probability that all the oranges are good
⇒
P (A ∩ B ∩ C) = 12/15 × 11/14 × 10/13 = 44/91
Hence, the probability that a box will be approved for sale = 44/91
4. A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B are independent events or not.
Solution:
Given, a fair coin and an unbiased die are tossed.
We know that the sample space S.
S = {(H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
Let A be the event head that appears on the coin.
⇒
A = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}
⇒
P (A) = 6/12 = ½
Now, Let B be the event 3 on the die.
⇒
B = {(H, 3), (T, 3)}
⇒
P (B) = 2/12 = 1/6
As, A ∩ B = {(H, 3)}
⇒
P (A ∩ B) = 1/12 …… (1)
And P (A). P (B) = ½ × 1/6 = 1/12 …… (2)
From (1) and (2) P (A ∩ B) = P (A). P (B)
Therefore, A and B are independent events.
5. A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event, ‘the number is even’, and B be the event, ‘the number is red’. Are A and B independent?
Solution:
The sample space for the dice will be
S = {1, 2, 3, 4, 5, 6}
Let A be the event, and the number is even.
⇒
A = {2, 4, 6}
⇒
P (A) = 3/6 = ½
Now, let B be the event, and the number is red.
⇒
B = {1, 2, 3}
⇒
P (B) = 3/6 = 1/2
As, A ∩ B = {2}
⇒
P (A ∩ B) = 1/6 …….. (1)
And P (A). P (B) = ½ × ½ = ¼ ….. (2)
From (1) and (2) P (A ∩ B) ≠ P (A). P (B)
Therefore, A and B are not independent events.
6. Let E and F be events with P (E) = 3/5, P (F) = 3/10 and P (E ∩ F) = 1/5. Are E and F independent?
Solution:
Given P (E) = 3/5, P (F) = 3/10 and P (E ∩ F) = 1/5
P (E). P (F) = 3/5 × 3/10 = 9/50 ≠ 1/5
⇒
P (E ∩ F) ≠ P (E). P (F)
Therefore, E and F are not independent events.
7. Given that the events A and B are such that P (A) = 1/2, P (A
∪
B) = 3/5 and P (B) = p. Find p if they are (i) mutually exclusive (ii) independent.
Solution:
Given, P (A) = ½, P (A
∪
B) = 1/5 and P (B) = p
(i) Mutually exclusive
When A and B are mutually exclusive.
Then, (A ∩ B) = ϕ
⇒
P (A ∩ B) = 0
As we know, P (A
∪
B) = P (A) + P (B) – P (A ∩ B)
⇒
3/5 = ½ + p -0
⇒
P = 3/5 – ½ = 1/10
(ii)
Independent
When A and B are independent.
⇒
P (A ∩ B) = P (A). P (B)
⇒
P (A ∩ B) = ½ p
As we know, P (A
∪
B) = P (A) + P (B) – P (A ∩ B)
⇒
3/5 = ½ + 2 – p/2
⇒
p/2 = 3/5 – ½
⇒
p = 2 × 1/10 = 1/5
8. If A and B are two events such that P (A) = 1/4 , P (B) = 1/2 and P (A ∩ B) = 1/8, find P (not A and not B).
Solution:
Given P (A) = ¼, P (B) = ½ and P (A ∩ B) = 1/8
P (not A and not B) = P (A
’
∩ B
’
)
As, { A
’
∩ B
’
= (A
∪
B)
’
}
⇒
P (not A and not B) = P ((A
∪
B)
’
)
= 1 – P (A
∪
B)
= 1- [P (A) + P (B) – P (A ∩ B)]
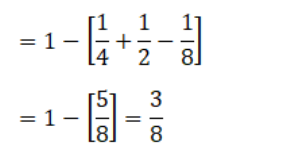 9. Events A and B are such that P (A) = 1/2, P (B) = 7/12 and P (not A or not B) = 1/4. State whether A and B are independent.
Solution:
Given P (A) = ½, P (B) =7/12 and P (not A or not B) = 1/4
⇒
P (A
’
∪
B
’
) = 1/4
⇒
P (A ∩ B)
’
= 1/4
⇒
1 – P (A ∩ B) = 1/4
⇒
P (A ∩ B) = 1 – 1/4
⇒
P (A ∩ B) = 3/4…….. (1)
And P (A). P (B) = ½ × 7/12 = 7/24 …. (2)
From (1) and (2) P (A ∩ B) ≠ P (A). P (B)
Therefore, A and B are not independent events.
9. Events A and B are such that P (A) = 1/2, P (B) = 7/12 and P (not A or not B) = 1/4. State whether A and B are independent.
Solution:
Given P (A) = ½, P (B) =7/12 and P (not A or not B) = 1/4
⇒
P (A
’
∪
B
’
) = 1/4
⇒
P (A ∩ B)
’
= 1/4
⇒
1 – P (A ∩ B) = 1/4
⇒
P (A ∩ B) = 1 – 1/4
⇒
P (A ∩ B) = 3/4…….. (1)
And P (A). P (B) = ½ × 7/12 = 7/24 …. (2)
From (1) and (2) P (A ∩ B) ≠ P (A). P (B)
Therefore, A and B are not independent events.
NCERT Solutions for Class 12 Maths Chapter 13 Probability Topic-Wise Discussion
The following major concepts of Maths that Probability class 12 Chapter 13 covers are included here.13.1 Introduction
13.2 Conditional Probability
13.2.1 Properties of Conditional Probability
13.3 Multiplication Theorem on Probability
13.4 Independent Events
13.5 Bayes’ Theorem
13.5.1 Partition of a Sample Space
13.5.2 Theorem of Total Probability
13.6 Random Variables and Their Probability Distributions
13.6.1 Probability Distribution of a Random Variable
13.6.2 Mean of a Random Variable
13.6.3 Variance of a Random Variable
13.7 Bernoulli Trials and Binomial Distribution
13.7.1 Bernoulli Trials
13.7.2 Binomial Distribution
The chapter on Probability is an entire unit, Unit 6—Probability carrying 8 marks of the total of 80 marks. To help students understand the concept of Probability thoroughly, this chapter includes 2 exercises as well as miscellaneous exercises. 1. 0 ≤ P (E|F) ≤ 1, P (E′|F) = 1 – P (E|F)P ((E ∪ F)|G) = P (E|G) + P (F|G) – P ((E ∩ F)|G) 2. P (E ∩ F) = P (E) P (F|E), P (E) ≠ 0P (E ∩ F) = P (F) P (E|F), P (F) ≠ 0 3. If E and F are independent, then P (E ∩ F) = P (E) P (F)P (E|F) = P (E), P (F) ≠ 0P (F|E) = P (F), P(E) ≠ 0 4. The theorem of total probability 5. Bayes’ theorem 6. A random variable is a real-valued function whose domain is the sample space of a random experiment. 7. Var (X) = E (X 2 ) – [E(X)] 2 8. Trials of a random experiment are called Bernoulli trials if they satisfy the following conditions :- There should be a finite number of trials.
- The trials should be independent.
- Each trial has exactly two outcomes: success or failure.
- The probability of success remains the same in each trial.
NCERT Solutions for Class 12 Maths Chapter 13 FAQs
What is the concept of conditional probability Maths class 12 Chapter 13 Probability?
The probability of events occurring in relation to a single event or more is defined as conditional probability. Considering that two events A and B are linked to the same sample space of a random experiment, the conditional probability of event A shall be decided by which event B occurs.
How are the NCERT Solutions for Class 12 Maths Chapter 13 helpful when it comes to students scoring well in the board exams?
Very simple language has been used to explain all the important concepts bearing in mind that these will be the answers in an exam. Students can analyse where they are lacking when they cross-check their answers with the NCERT Solutions for Class 12 Maths Chapter 13 given here.
How can I score good marks in class 12 Maths Probability?
Students shall have to practice regularly and seek help from their teachers and the peer group. There’s no substitute for regular practice as such practice helps remove any confusion about the many concepts included in Maths Class 12 Chapter 13 Probability.
What are the chances of scoring well in the exams with these solutions?
The solutions to the problems in Maths Class 12 Chapter 13 Probability have been given by experts in the field of Statistics. Their detailed explanations of the problems are sure to fetch good marks.
How helpful are the explanations here in overcoming the fear of Statistics?
With the explanations having been given keeping in mind the challenges faced by weaker students, the exercises here from our experts do help students deal with the fear of studying Maths a great deal.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









