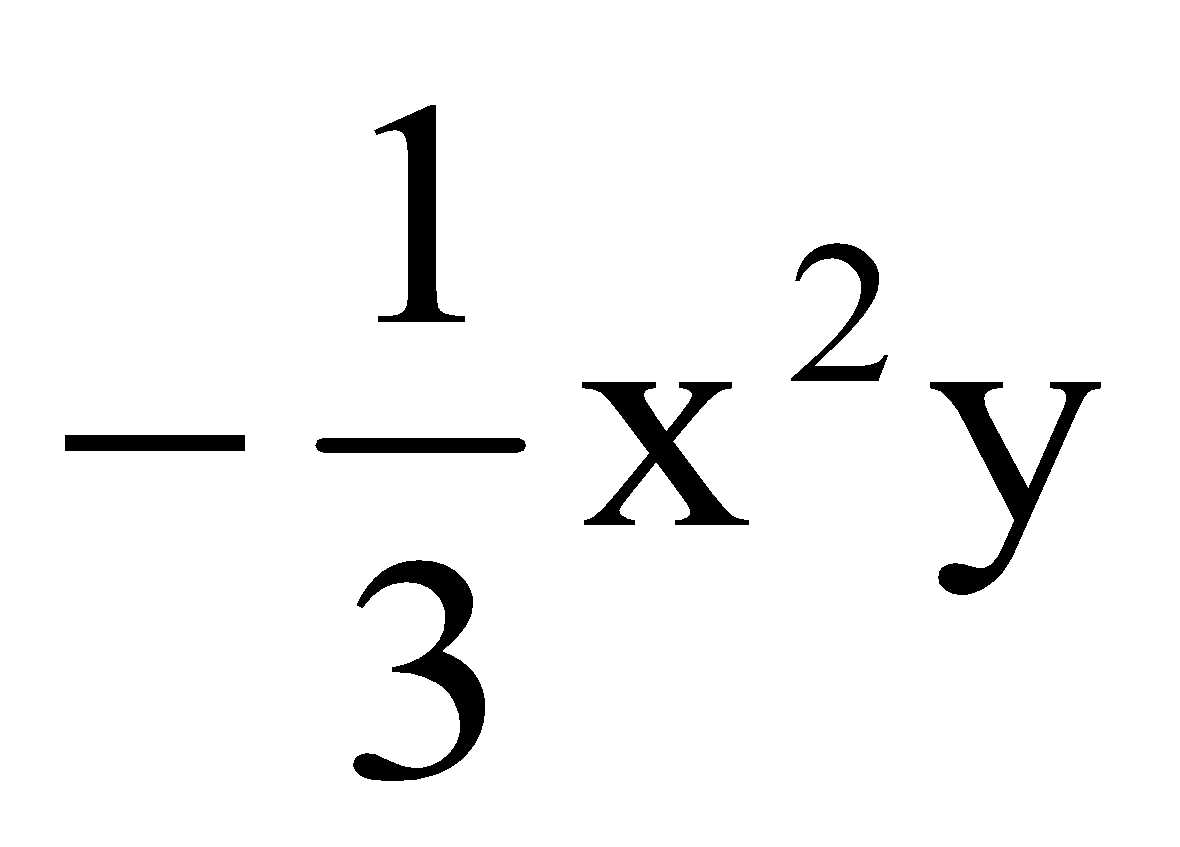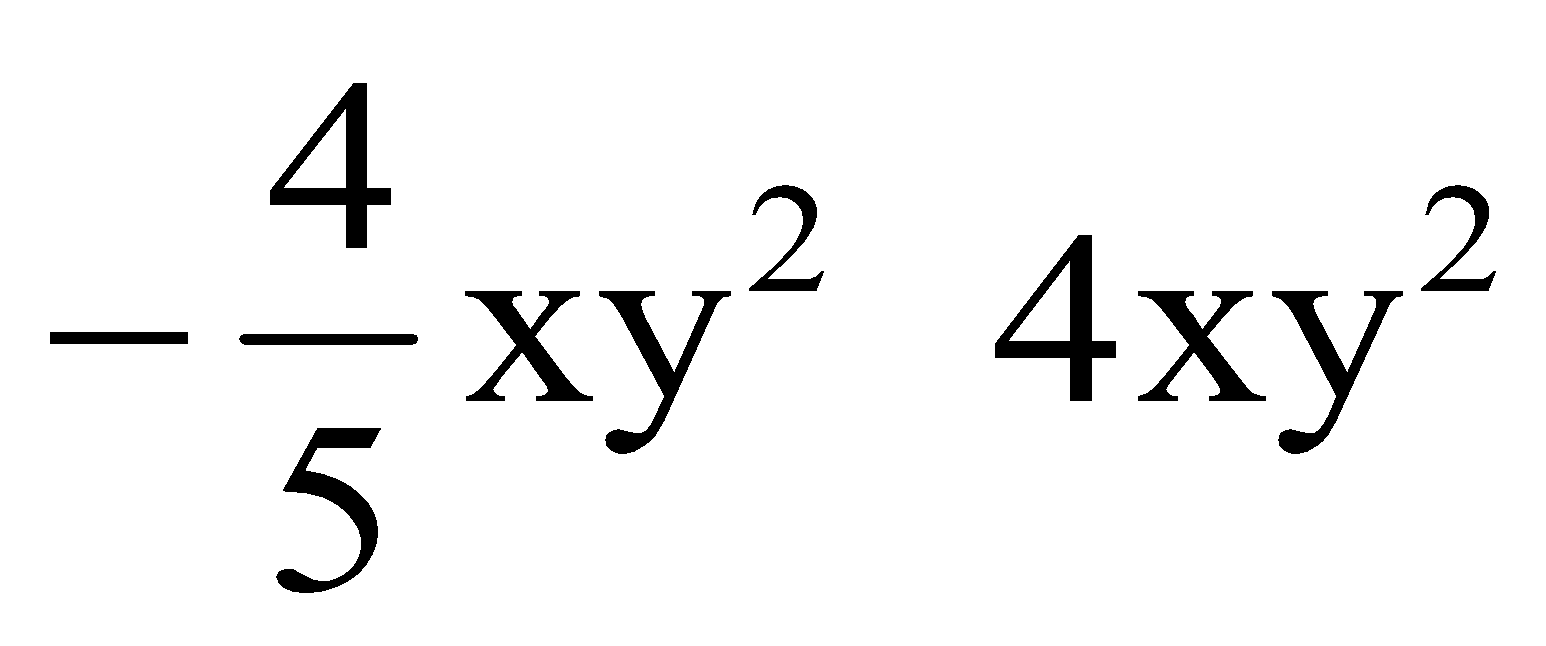simplifying expressions examples

Exponents are used in many algebra problems, so it's important that we understand the rules for working with exponents. Let's go over each rule in detail, and see some examples.

RULES OF 1:

There are two simple "rules of 1" to remember.

First, any number raised to the power of "one" equals itself. This makes sense, because the power shows how many times the base is multiplied by itself. If it's only multiplied one time, then it's logical that it equals itself.

Secondly, one raised to any power is one. This, too, is logical, because one times one times one, as many times as you multiply it, is always equal to one.

x1 = x

31 = 3

1m = 1

14 = 1 ⋅ 1 ⋅ 1 ⋅ 1

= 1

PRODUCT RULE:

The exponent "product rule" tells us that, when multiplying two powers that have the same base, you can add the exponents. In this example, you can see how it works. Adding the exponents is just a short cut!

xm⋅ xn = xm + n

42⋅ 43 = 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4

42 + 3 = 45

POWER RULE:

The "power rule" tells us that to raise a power to a power, just multiply the exponents. Here you see that 52 raised to the 3rd power is equal to 56.

  xmn = xmn

(52)3 = 52 × 3 = 56

QUOTIENT RULE:

The quotient rule tells us that we can divide two powers with the same base by subtracting the exponents. You can see why this works if you study the example shown.

xm÷ xn = xm – n

x ≠ 0

45÷ 42 =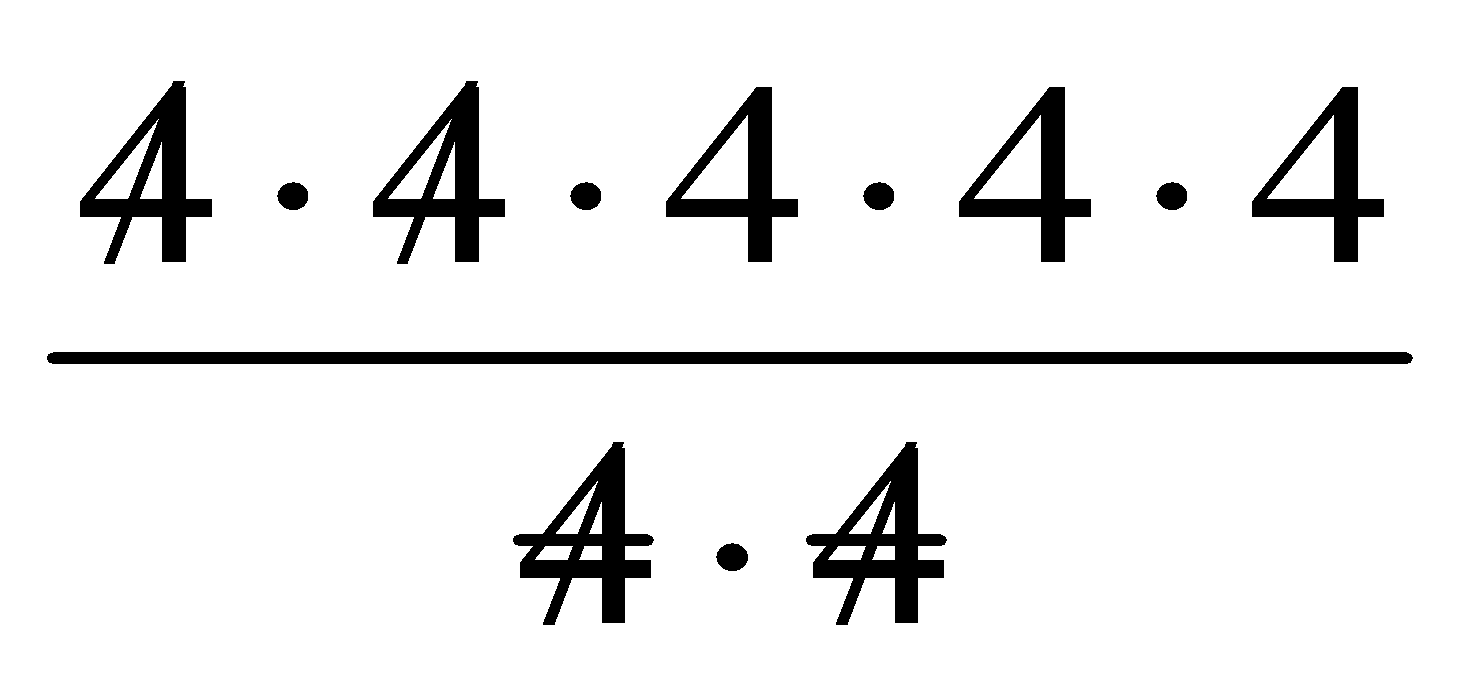

45 – 2 = 43

ZERO RULE:

According to the "zero rule," any nonzero number raised to the power of zero equals 1.

xo = 1

x ≠ 0

NEGATIVE EXPONENTS:

The last rule in this lesson tells us that any nonzero number raised to a negative power equals its reciprocal raised to the opposite positive power.

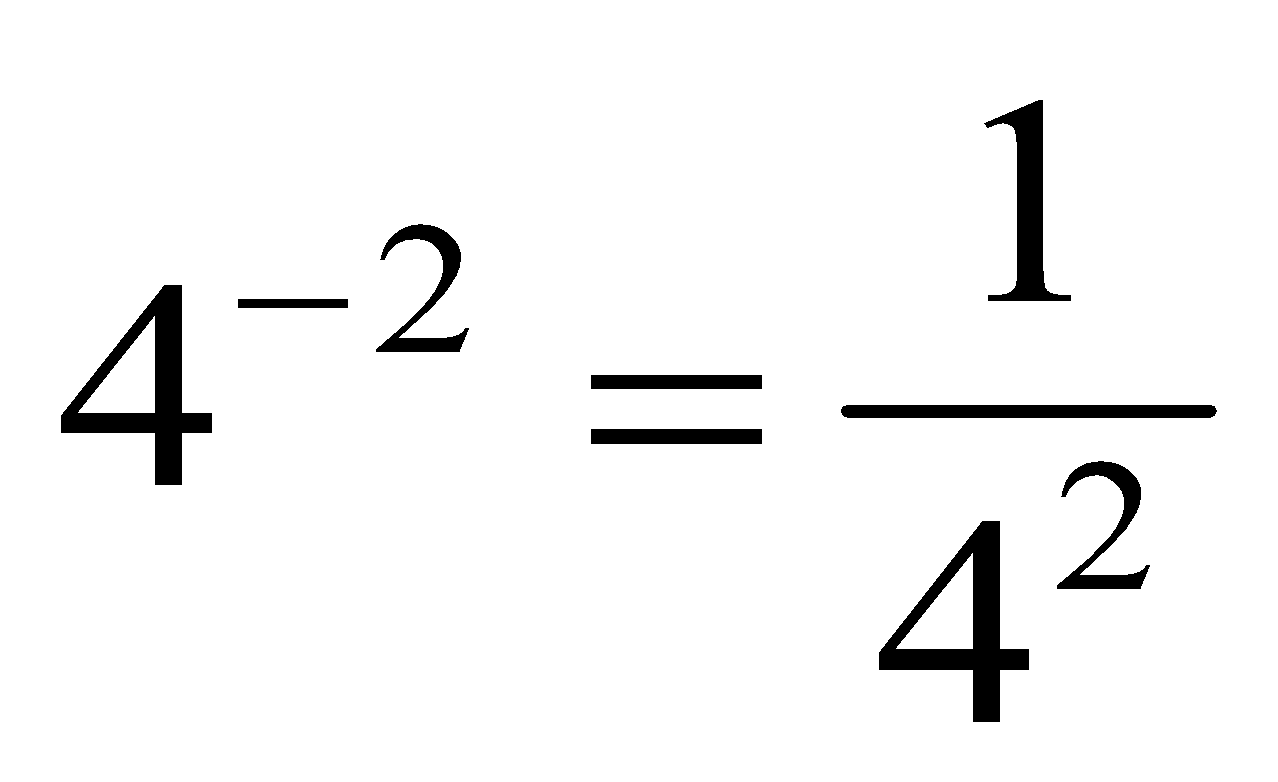
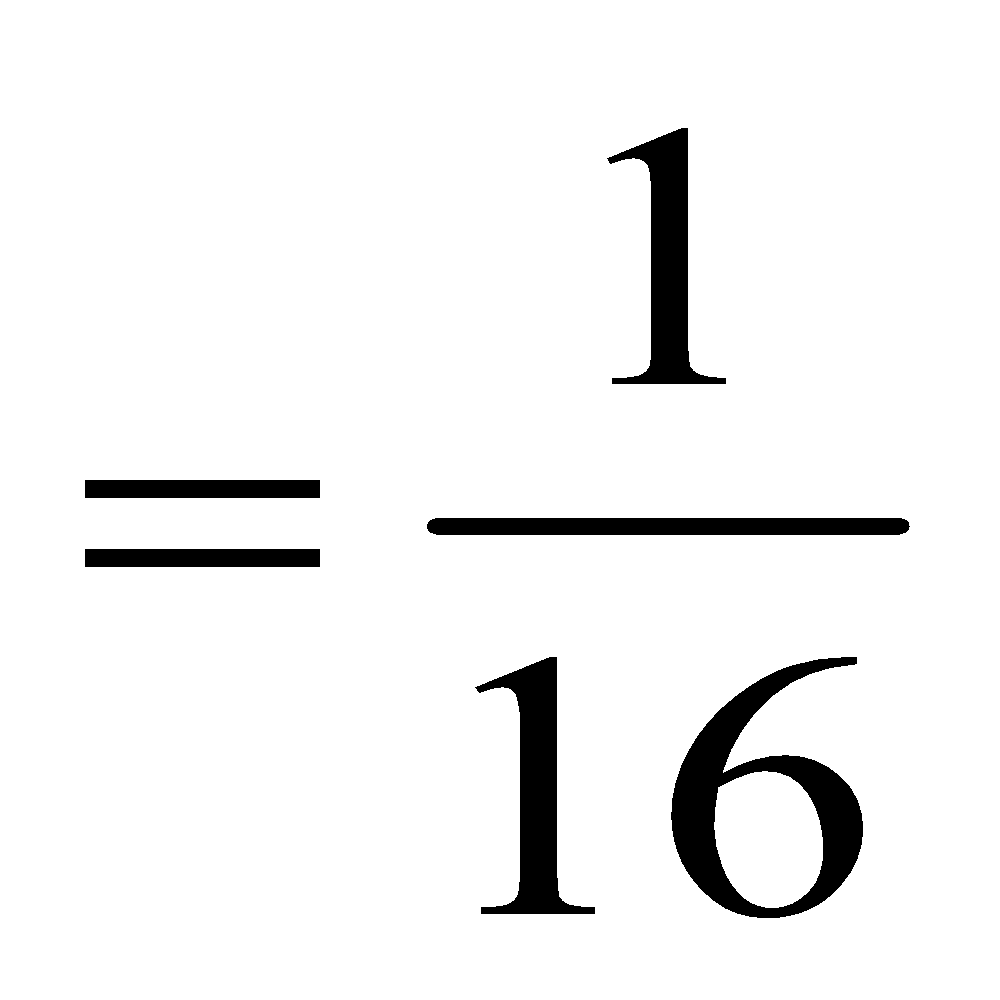
e.g. Simplify (x3)(x4)

To simplify this, I can think in terms of what those exponents mean. "To the third" means "multiplying three copies" and "to the fourth" means "multiplying four copies". Using this fact, I can "expand" the two factors, and then work backwards to the simplified form:

(x3)(x4)= (xxx)(xxxx) 

 = xxxxxxx 
 = x7

Note that x7 also equals x(3+4). This demonstrates the first basic exponent rule: Whenever you multiply two terms with the same base, you can add the exponents:

( x m ) ( x n ) = x( m + n )

However, we can NOT simplify (x4)(y3), because the bases are different: (x4)(y3) = xxxxyyy = (x4)(y3). Nothing combines.

question 1. Simplify (x2)4

Solution: Just as with the previous exercise, I can think in terms of what the exponents mean. The "to the fourth" means that I'm multiplying four copies of x2:

(x2)4 =(x2)(x2)(x2)(x2) 
 =(xx)(xx)(xx)(xx) 
 = xxxxxxxx 
 = x8

Note that x8 also equals x( 2×4 ). This demonstrates the second exponent rule: Whenever you have an exponent expression that is raised to a power, you can multiply the exponent and power:

( xm ) n = x m n

If you have a product inside parentheses, and a power on the parentheses, then the power goes on each element inside. For instance, (xy2)3 = (xy2)(xy2)(xy2) = (xxx)(y2y2y2) = (xxx)(yyyyyy) = x3y6 = (x)3(y2)3. Another example would be:

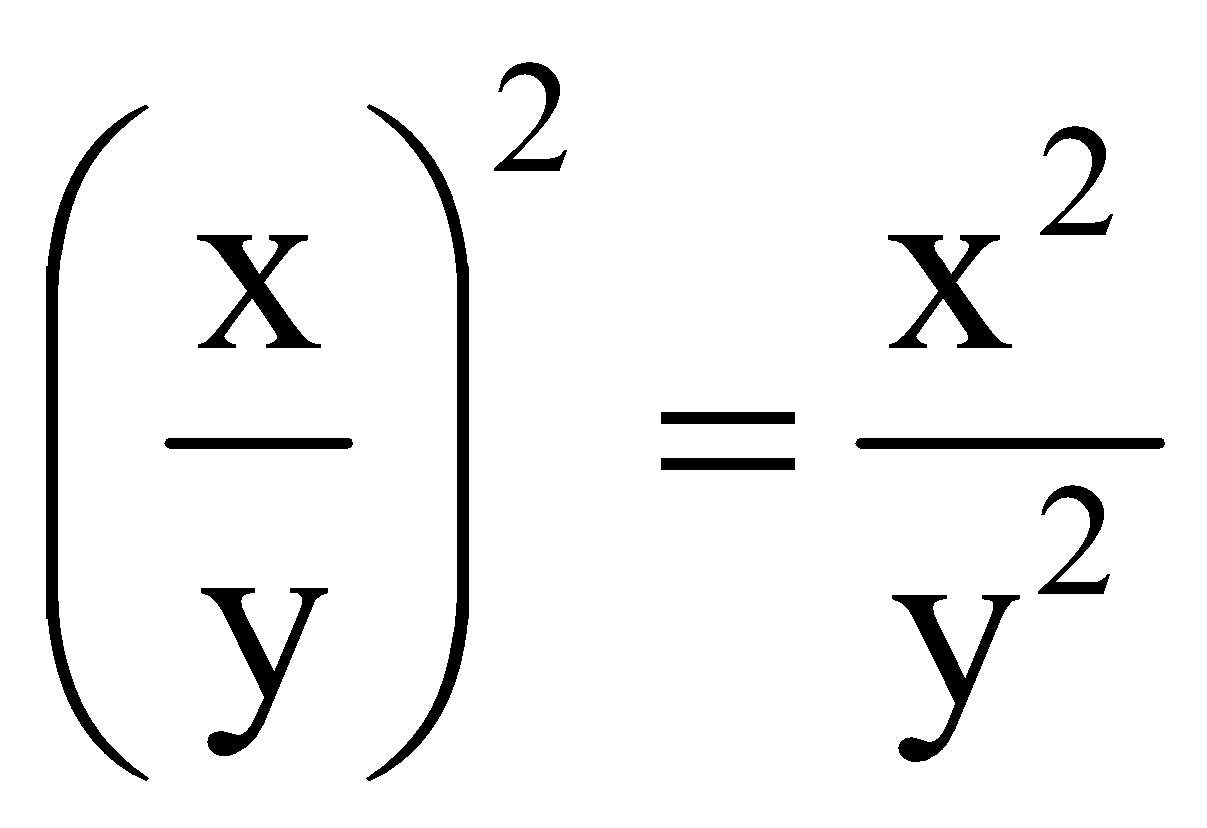
question 2. Simplify [(3x4y7z12)5 (–5x9y3z4)2]0

Anything to the power zero is just "1".

Solution: The zero power on the outside means that the value of the entire thing is just 1.

question 3. Evaluate 2x3 – x2 + y for x = –3, y = 2.

Solution: 2x3 – x2 + y = 2 (–3)3 – (–3)2 + 2 Replace each x with –3, each y with 2.

= 2 (–27) – (9) + 2 Perform the indicated operations.

= –54 – 9 + 2

= –61

question 4. Evaluate x2 – x3y + 6 for x = 2, y = 9

Sol. x2 – x3y + 6 = (2)2 – (2)3⋅ (9) + 6 Put values in parentheses

= 4 – 8 ⋅ 9 + 6 Do operations involving exponents

= 4 – 72 + 6 Do multiplication

= –62

question5 . To illustrate the important of enclosing the substituted values in parentheses, let’s evaluate 2x3 – x2 + y for x = –3, y = 2 without using parentheses:

2x3 – x2 + y = 2 – 33 – 32 + 2

Solution: In the resulting expression on the right, it’s difficult to keep track of the negative signs and the indicated operations. It’s easy to see how errors can occurs without parentheses.

LIKE TERMS:

Like terms are terms that contain the same variables raised to the same power. Only the numerical coefficients are different. In an expression, only like terms can be combined. We combine like terms to shorten and simplify algebraic expressions, so we can work with them more easily. To combine like terms, we add the coefficients and keep the variables the same. We can't combine unlike terms because that's like trying to add apples and oranges!

Look at these 10 terms. Let's find all the like terms that can be combined.

3 x2y 2x2y2 –2xy2

4xy2 –7x2yz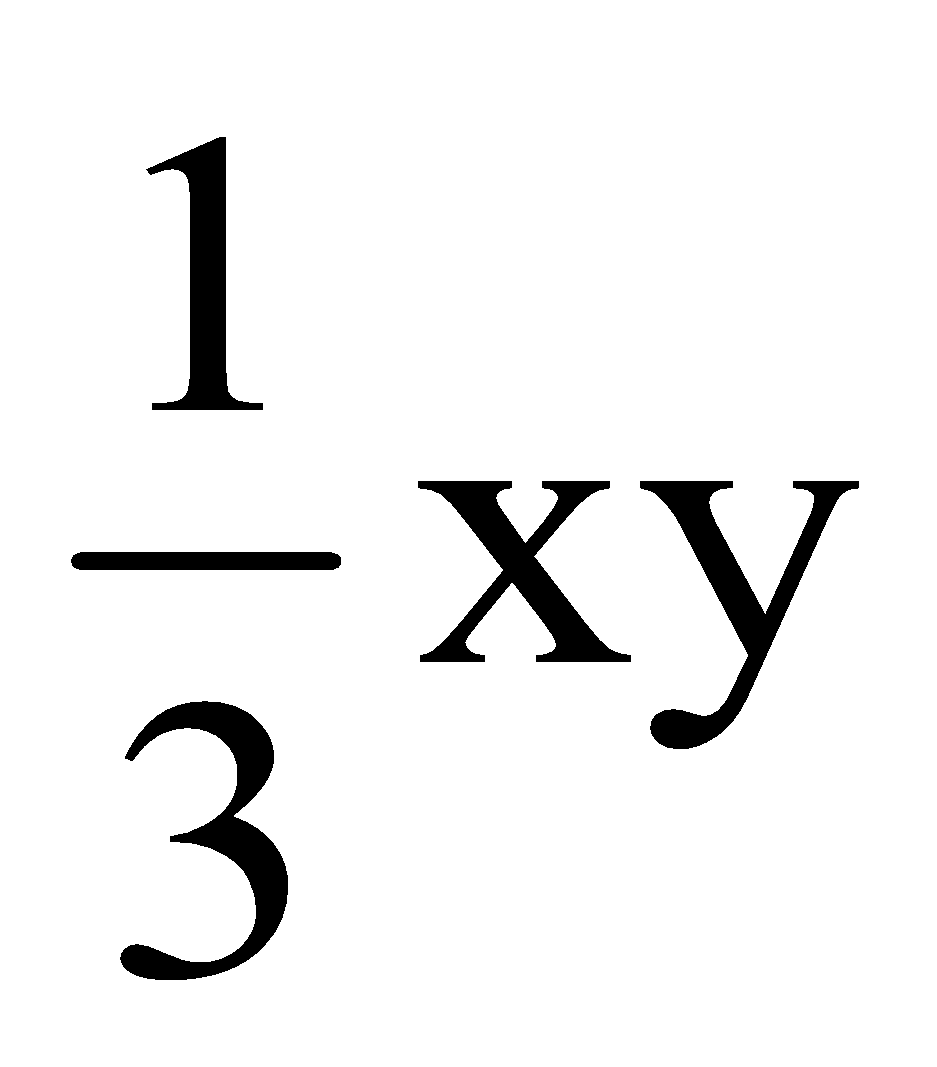

–8x2y –5xy2z

Be careful when combining! 

Terms like x2yz and xy2z look a lot alike, but they aren't and cannot be combined. Write the terms carefully when working out problems.

Don't overlook terms that are alike!

Terms obey the associative property of multiplication - that is, xy and yx are like terms, as are xy2 and y2x.

COMBINE LIKE TERMS:

question 1. 5x – 2y + 3x – 7y

= 8x – 2y – 7y Combine the terms with the variable x.

= 8x – 9y Combine the terms with the variable y

question 2. 8x3y2 + 3x3 – 7x2y3 + 9x3y2

= (8 + 9)x3y2 + 3x3 – 7x2y3 Combine the terms with the variables x3y2.

= 17x3y2 + 3x3 – 7x2y3 All like terms are combined

SIMPLIFYING

Before you evaluate an algebraic expression, you need to simplify it. This will make all your calculations much easier. Here are the basic steps to follow to simplify an algebraic expression:

• remove parentheses by multiplying factors
• use exponent rules to remove parentheses in terms with exponents
• combine like terms by adding coefficients
• combine the constants

Let's work through an example.

5(2 + x) + 3(5x + 4) – (x2)2

When simplifying an expression, the first thing to look for is whether you can clear any parentheses. Often, you can use the distributive property to clear parentheses, by multiplying the factors times the terms inside the parentheses. In this expression, we can use the distributive property to get rid of the first two sets of parentheses.

= 10 + 5x + 15x + 12 – (x2)2

Now we can get rid of the parentheses in the term with the exponents by using the exponent rules we learned earlier. When a term with an exponent is raised to a power, we multiply the exponents, so (x2)2 becomes x4.

= 10 + 5x + 15x + 12 – x4

The next step in simplifying is to look for like terms and combine them. The terms 5x and 15x are like terms, because they have the same variable raised to the same power -- namely, the first power, since the exponent is understood to be 1. We can combine these two terms to get 20x.

= 10 + 20x + 12 – x4

Finally, we look for any constants that we can combine. Here, we have the constants 10 and 12. We can combine them to get 22.

= 22 + 20x – x4

Now our expression is simplified. Just one more thing -- usually we write an algebraic expression in a certain order. We start with the terms that have the largest exponents and work our way down to the constants. Using the commutative property of addition, we can rearrange the terms and put this expression in correct order, like this.

= –x4 + 20x + 22