Equations containing fractions
Share
Equations containing fractions
Linear equations in one variable of Class 8
To solve for x in an equation such asfirst clear the equation of fraction, To do this, find the least common denominator of the fraction. Then multiply both rider of the equation by the LCD. The least common denominator of 3, 12, 4, and 2 is 12. Multiply both rider of the equation by 12. The resulting equation is
8x + x - 12 - 3 + 8x
Subtract 6x from both members, add 12 to both members, and collect like terms as follows:
9x – 6x = 12 + 3
3x = 15
The solution is
x= 5
To prove that x = 5 is the correct solution, substitute 5 for x in the original equation and show that both sides of the equation reduce to the same value. The result of substitution is
In establishing an identity, the two sides of the equality are treated separately, and the op the equality, and it is desirable to find the least common denominator for more than one set of fractions. The same denominator could be used on both sides of the equality, but this might make some of the terms of the fractions larger than necessary.
Proceeding in establishing the identity for x = 5 in the foregoing equation we obtain
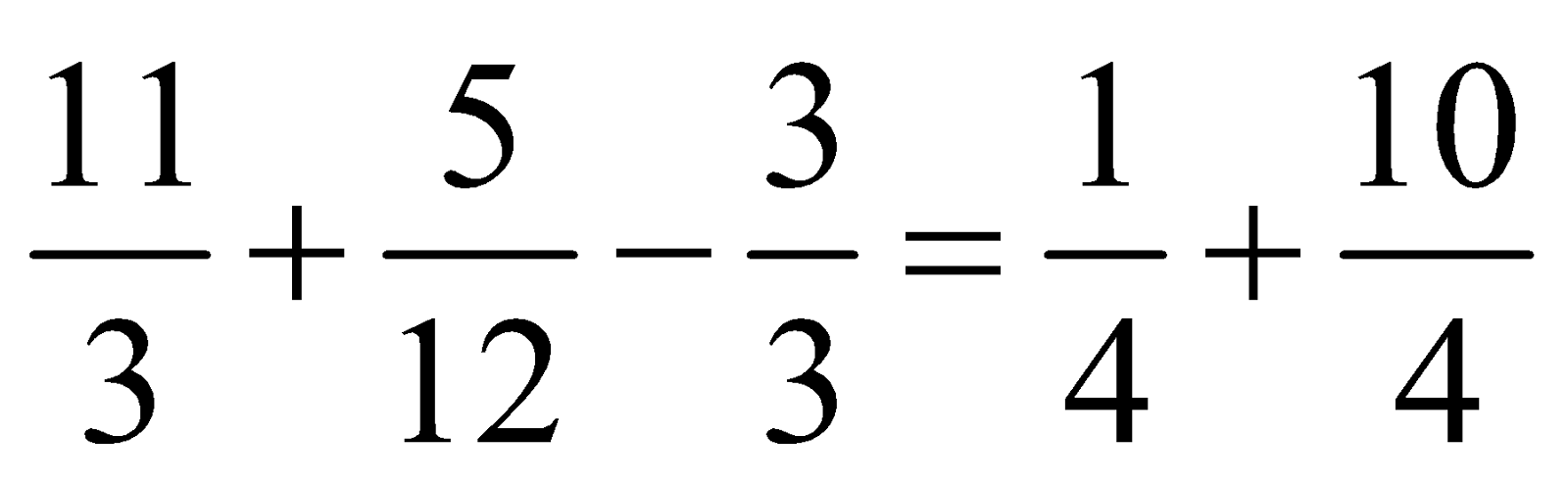
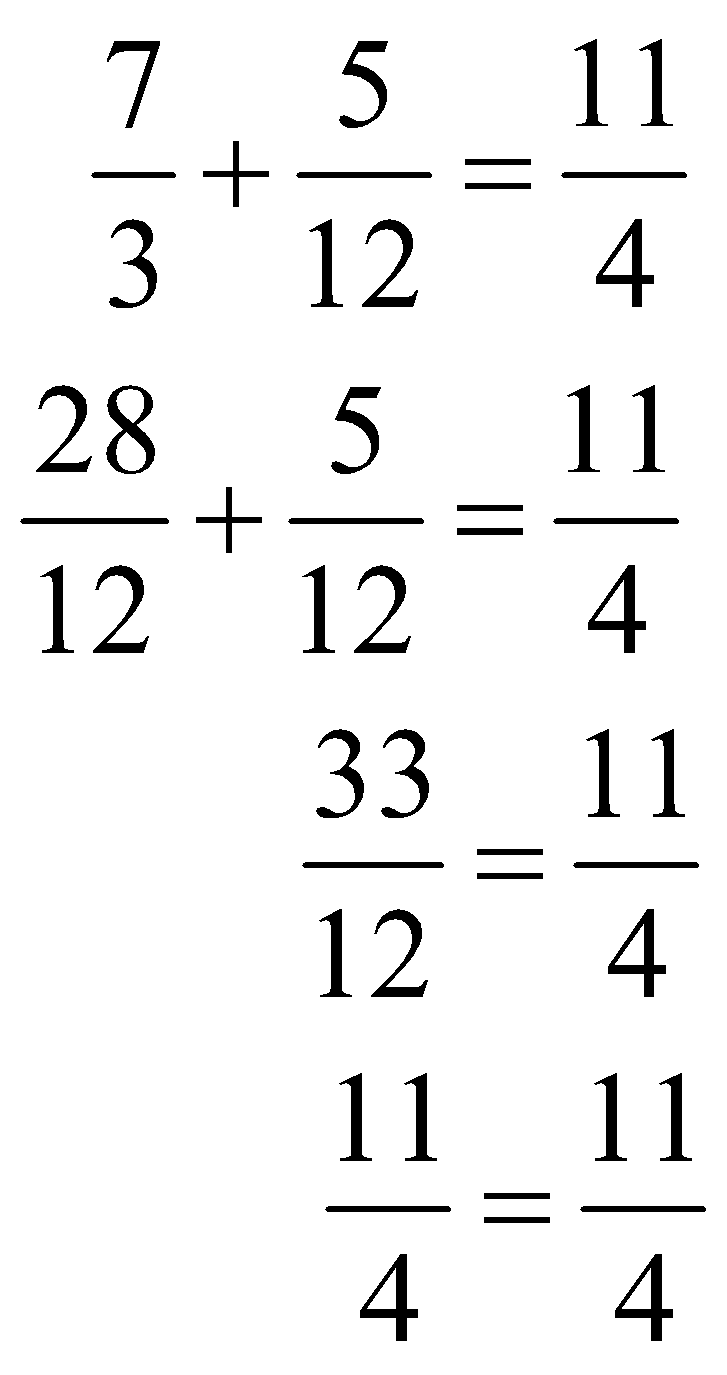
Each member of the equality has the value 11/4 when x = 5. The fact that the equation be proves that x = 5 is the solution.
