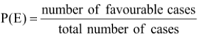Some Special Sample Spaces

question 1. A die is thrown once. What is the probability of getting a prime number?

Solution: In a single throw of a die, all possible outcomes are 1, 2, 3, 4, 5, 6.

Total number of possible outcomes = 6.

Let E be the event of getting a prime number.

Then, the favourable outcomes are 2, 3, 5.

Number of favourable outcomes = 3.

∴ P(getting a prime number) = P(E) = 3/6 = 1/2

question 2. A coin is tossed once. What is the probability of getting a head?

Solution: When a coin is tossed once, all possible outcomes are H and T.

Total number of possible outcomes = 2.

The favourable outcome is H.

Number of favourable outcome = 1

∴ P(getting a head)

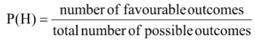= 1/2

question 3. A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the

(i) Yellow ball?

(ii) Red ball?

(iii) Blue ball?

Solution: Kritika takes out a ball from the bag without looking into it. So, it is equally likely that she takes out any one of them.

Let Y be the event ‘the ball taken out is yellow’, B be the event ‘the ball taken out is blue’, and R be the event ‘the ball taken out is red’.

Now, the number of possible outcomes = 3.

(i) The number of outcomes favourable to the event Y = 1.

So, P(Y) = 1/3

Similarly, (ii) P(R) = 1/3 and (iii) P(B) = 1/3

question 4. All the three face cards of spades are removed from a well-shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting.

(i) Black face card (ii) a queen (iii) a black card.

Solution: After removing three face cards of spades (king, queen, and jack) from a deck of 52 playing cards, there are 49 cards left in the pack. Out of these 49 cards one card can be chosen in 49 ways.

∴ Total number of elementary events = 49

(i) There are 6 black face cards out of which 3 face cards of spades are already removed. So, out of remaining 3 black face cards one black face card can be chosen in 3 ways.

∴ Favourable number of elementary events = 3

Hence, P (getting a black face card) = 3/49

(ii) There are 3 queens in the remaining 49 cards. So, out of these three queens, one queen can be chosen in 3 ways

∴ Favourable number of elementary events = 3

Hence, P (Getting a queen) = 3/49

(iii) There are 23 black cards in the remaining 49 cards. So, out of these 23 black cards, one black card can be chosen in 23 ways

∴ Favourable number of elementary events = 23

Hence, P (Getting a black card) = 23/49

question 5. A die is thrown, Find the probability of

(i) prime number (ii) multiple of 2 or 3 (iii) a number greater than 3

Solution: In a single throw of die any one of six numbers 1,2,3,4,5,6 can be obtained. Therefore, the tome number of elementary events associated with the random experiment of throwing a die is 6.

(i) Let A denote the event “Getting a prime no”. Clearly, event A occurs if any one of 2,3,5 comes as outcome.

∴ Favorable number of elementary events = 3

Hence, P (Getting a prime no.) = 3/6 = 1/2

(ii) An multiple of 2 or 3 is obtained if we obtain one of the numbers 2,3,4,6 as out comes

∴ Favorable number of elementary events = 4

Hence, P (Getting multiple of 2 or 3) = 4/6 = 2/3

(iii) The event “Getting a number greater than 3” will occur, if we obtain one of number 4,5,6 as an outcome.

∴ Favorable number of outcomes = 3

Hence, required probability = 3/6 = 1/2

question 6. Two unbiased coins are tossed simultaneously. Find the probability of getting

(i) two heads (ii) at least one head (iii) at most one head

Solution: If two unbiased coins are tossed simultaneously, we obtain any one of the following as an outcome:

HH, HT, TH, TT

∴ Total number of elementary events = 4

(i) Two heads are obtained if elementary event HH occurs.

∴ Favorable number of events = 1

Hence, P (Two heads) = 1/4

(ii) At least one head is obtained if any one of the following elementary events happen :

HH, HT, TH

∴ favorable number of events = 3

Hence P (At least one head) = 3/4

(iii) If one of the elementary events HT, TH, TT occurs, than at most one head is obtained

∴ favorable number of events = 3

Hence, P (At most one head) = 3/4

question 7. Two coins are tossed simultaneously. What is the probability of getting at least one head?

Solution: When two coins are tossed simultaneously, all possible outcomes are HH, HT, TH, TT.

Total number of possible outcomes = 4.

Let E be the event of getting at least one head.

Then, the favourable outcomes are HT, TH, HH.

Number of favourable outcomes = 3.

∴ P(getting at least one head) = P(E) = 3/4.

question 8. One card is drawn at random from a well-shuffled deck of 52 cards. What is the probability that the card drawn is a face card?

Solution: Total number of all possible outcomes = 52.

We know that kings, queens and jacks are the face cards.

Number of face cards = 12.

Let E be the event of getting a face card.

Then, the number of favourable outcomes = 12.

∴ P(getting a face card) = 12/52 = 3/13

question 9. Cards each marked with one of the numbers, 4, 5, 6, …., 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box. What is the probability of getting an even prime number?

Solution: Out of 17 (= 20 − 3) cards, one card can be drawn in 17 ways.

∴ Total number of possible outcomes = 17

There are 6 prime numbers, namely, 5, 7, 11, 13, 17, 19

Here, there is no even prime number.

∴ Favourable number of outcomes out of 17 = 0

Hence, P(getting an even prime number) = 0/17 = 0