Set Theory and Inclusion-Exclusion Principle

Set Theory and Inclusion - Exclusion Principle

(a) P(AB) = P(A) + P(B) - P(AB)

(b) 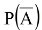=1 - P(A)

(c) P(ABC) = P(A) + P(B) + P(C) - P(AB) - P(AC) - P(BC) + P(ABC)

(d) 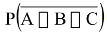= 1 - P(A) - P(B) - P(C) + P(AB) + P(AC) + P(BC) - P(ABC)

An important class of questions asked in probability are those in which it is required to prove that certain events are independent or mutually exclusive.

Proceed as follows :

For independence of events, find P(A), P(B) and P(AB)

Verify that P(AB) = P(A). P(B)

while for mutual exclusiveness, find P(AB) and show that P(AB) = 0

OR find P(AB), P(A) & P(B) and show that P(AB) = P(A) + P(B).

Note : One important distinction has to be made between pairwise independence and
independence in general. Events A₁ ,..., A_n are pairwise independent if
P(A_i  A_j) = P(A_i). P(A_j)  i, j, i  j, i, j  {1,...,n}

and A₁ ,..., A_n are independent if for all k , 2 ≤ k ≤ n

Hence independence  pair wise independence

But not necessarily the other way round.