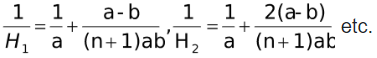Harmonic Progressions (HP)
sequence and series of Class 11
Harmonic Progressions (HP)
A sequence a1 a2 . . . an is said to be in HP if 
is in AP
i.e. an =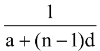 
where a = 
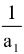and d = 
.
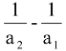(a) The harmonic mean of two nonzero numbers a and b is H then obviously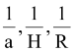 
are in HP and therefore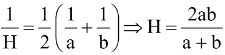 
The idea can be extended to the H.M. of n such numbers as
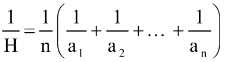
(b) If n HM’s are inserted between a & b then a, H1, H2 . . . Hn, b are in HP
i.e.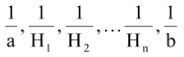 
are in AP with common difference d (say).
Then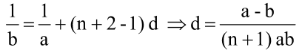 
Then 
