Differentiation of determinant

Jul 27, 2022, 16:45 IST

About Differentiation of determinant

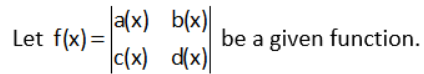
Where a(x), b(x), c(x), d(x) are functions of x.

Then, when we will expand f(x) with the help of the property of the determinant, we get

f(x) = a(x) d(x) – c(x) b(x)

Now, upon differentiating both sides, we get

f’(x) [’(x) d(x) + a(x)d’(x)] – [c’(x) b(x) + c(x) b’(x)]

f’(x) = a’(x) d(x) + a(x) d’(x) – c’(x) b(x) – c(x) b’(x)

Now, after rearrangement, we get

Case-1:

f’(x) = a’(x) d(x) – c’(x) b(x) + a(x) d’(x) – c(x) b’(x)

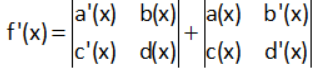
This is column differentiation.

Case-2:

f’(x) = a’(x) d(x) – c(x) b’(x) + a(x) d’(x) – c’(x) b(x)

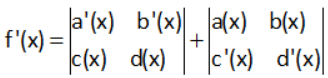
This is row differentiation.

Thus, the differential coefficient of a determinant is obtained by differentiating a single row (or column) at a time and finally adding the determinants so obtained. Thus, for a determinant of order 'n'.

Then

Do solve NCERT textbook with the help of Physics Wallah NCERT solutions for class 12 Maths.

Frequently Asked Question (FAQs)

Q1. How do you differentiate a determinant?

Ans. To differentiate a determinant, we first have to differentiate one row (or column) at a time, keeping others determinants unchanged. Eg: Let f(x) = | x ² + a ² a x ² + b ² b | , find F(x).

Q2. What is the formula of determinants?

Ans. The determinant is: |A| = a (ei − fh) − b (di − FG) + c (DH − eg). The determinant of A equals 'a times e x i minus f x h minus b times d x i minus f x g plus c times d x h minus e x g'.

Q3. What is the property of determinant?

Ans. There are ten main properties of determinants: reflection property, all-zero property, proportionality or repetition property, switching property, scalar multiple properties, sum property, invariance property, factor property, triangle property, and co-factor matrix property.

Q4. What is a determinant in a matrix?

Ans. The determinant of a matrix is the scalar value or number calculated using a square matrix. The square matrix could be 3×3, 4×4, 5×5, or any type, such as n × n, where the number of columns and rows are equal.

Q5. Is a matrix differentiable?

Ans. If the function is differentiable, then the derivative is simply a row matrix that contains all of these derivatives, which we call the matrix of the partial derivatives (also called the Jacobian matrix).

Q6. Is matrix important for JEE?

Ans. Yes, the Matrix and Determinants topic are essential for students planning to apply for advanced JEE Main exams. To maximize the marks for the JEE advanced exam, it is recommended that the student prepare well for all the essential topics covered in this chapter.

Q7. What are the three types of determinants?

Ans. There are commonly three types of determinants- First order determinant, Second-order determinant, and Third-order determinant.