Tangent and Normal
Application of derivatives of Class 12
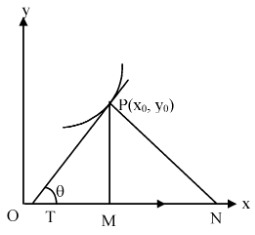
Let y = f(x) be the equation of a curve and let P(x0, y0) be a point on the curve. Let PT be the tangent, PN the normal and PM be perpendicular to the axis of x.
The slope of the tangent to the curve y = f(x) at P is given by 
|
and therefore the equation to the tangent to the curve y = f(x) at (x0, y0) is
y −y0 = and the equation to the normal will be
y −y0 + Length of the tangent is PT = y0 cosecθ |
|
= y0 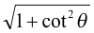 = y0
= y0 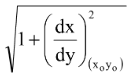
and length of the normal is
y0 secθ = y0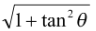 = y0
= y0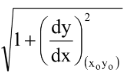
Likewise lengths of the subtangent and subnormal can also be calculated.
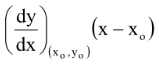
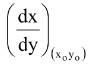 (x −xo) = 0
(x −xo) = 0