Derivatives

Derivatives

Right hand and left hand derivative of a function

The progressive derivative or right hand derivative of f(x) at x=a is given by

 if it exists finitely is denoted by f′(a+).

The regressive or left hand derivative is also like wise defined as

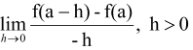
and is denoted by f ′(a-)

The function f(x) is said to be differentiable at x = a if f′ (a) and L f ′(a) exist at x = a and are equal and their common value is the Derivative or Differential coefficient at x = a.

The function is said to be non-differentiable at x = a if

(a) both f ′(a+) and f ′(a-) exists but are not equal

(b) either or both are not finite

(c) Either or both do not exist.