General form of variable separable differential equations
Differential Equations of Class 12
General form of variable separable differential equations
If we can write the differential equation as f1(f2(x)) d(f2(x)) + f3 (f4(x)) d(f4(x)) + ..... + f2n - 1 (f2n (x)) d (f2n (x)) = 0, where f1, f2,....., f2n are real valued function. Then integrate each term w.r.t f2(x), f4(x), ..... , f2n(x) respectively, we get the solution of the given differential equation for this the following derivatives must be remembered.
(i) d(x + y) = dx + dy (ii) d(xy) = y dx + x dy
(iii) d =  (iv) d
(iv) d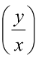 =
= 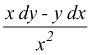
(v) d(log xy) = 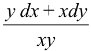 (vi) d
(vi) d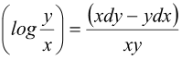
(vii) d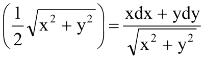
- Introduction
- Degree of a differential equation
- Formation of differential equation
- Solution of differential equation
- Different forms of first order and first degree differential equations
- General form of variable separable differential equations
- Some results on Tangents and Normals
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6









