Integration of Basic Irrational Functions

Integration of Trigonometric Functions

(a) To evaluate integrals of the form I = 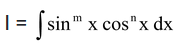where m and n are rational numbers.

(1) Substitute sin x = t if n is odd +ve integer

(2) cos x = t if m is odd +ve integer

(3) tan x = t if m+n is a –ve even integer

(b) Integrals of the form

where R is a rational function of sin x and cos x are transformed into integers of a rational function by the substitution.

where -π < x < π

we then have

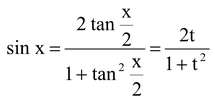
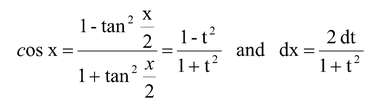
Certain functions may be extremely complex rational functions, but in most of the cases the integers can be simplified by the following substitution.

Substitute Integral of the form

(a) sin x = t R (sin x) . cos x dx

(b) cos x = t R (cos x) sin x dx

(c) tan x = t If the integral is dependent only on tan x

(d) tan x = t If the integrand has the form R (sin x cos x) but sin x and cos x appear only in even power.

(e) cos x = t If R(-sin x, cos x) = -R (sin x, cos x)

(f) sin x = t If R (sin x, - cos x) = - R (sin x, cos x)

Integration of Rational Functions

Every rational function can be represented in the form P(x) / Q(x) where P(x) and Q(x) are polynomials  i.e., 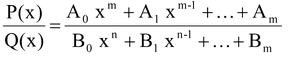assuming of course that the polynomials do not have any common root.

If the fraction is improper, then we can always write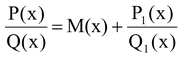

Just as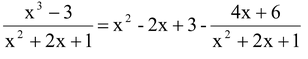

Few Cases

(a)

(b)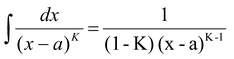

(c)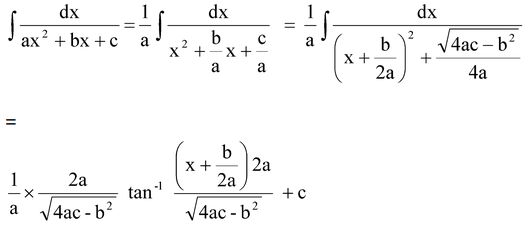

(d)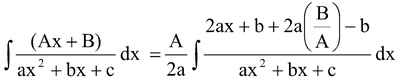

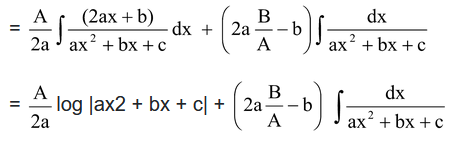
(e) If 4ac – b2 < 0 then (c) fails and we can reorganize.

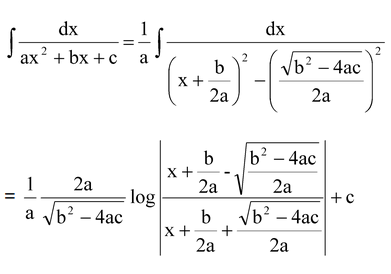
(f) If the integrand is not any of the above forms we decompose the expression into partial fractions and integral separately. For example, I =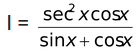

To start we change the expression to an algebraic one by putting tan x = t

we get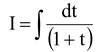  

= ln|1 + t| = ln |1 + tanx| + c