Identification of conics

Consider the general equation of second degree ax₂ + 2hxy + by₂ + 2gx + 2fy + c = 0 and the condition that it can be factorised into two linear factors is, Δ = abc + 2fgh − af₂ − bg₂ − ch₂ = 0.

Now, If Δ ≠ 0

Then

1. h = 0, a = b It represents a circle
2. ab − h₂ = 0 A parabola
3. ab − h₂ > 0 An ellipse
4. ab − h₂ < 0 A hyperbola

Centre of conics

If S = ax₂ + 2hxy + by₂ + 2gx + 2fy + c = 0

then = 0 and 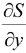= 0 represent the center of the conic that is solving
ax + hy + g = 0 and hx + by + f = 0.