Division Of A Line Segment

In order to divide a line segment internally is a given ratio m: n, where both m and n are positive integers,

We follow the following steps:

STEP OF CONSTRUCTION:

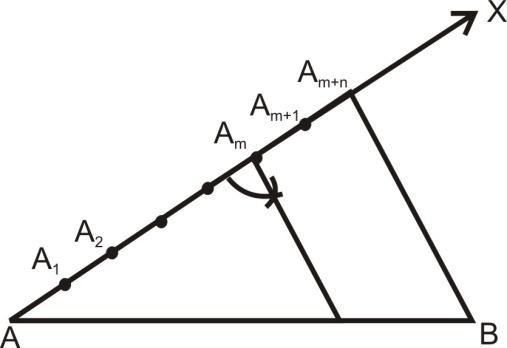
(i) Draw a line segment AB of given length by using a ruler.

(ii) Draw and ray AX making an acute angle with AB.

(iii) Along AX mark off (m + n) points A₁, A₂,..., Am+n such that AA₁ = A₁A₂ = ....= A_m+n+A_m+n.

(iv) Join B A_m+n

(v) Through the point Am draw a line parallel to Am+n B by making an angle equal to ∠AA_{m + n} Bat Am.

Suppose this line meets AB at a point P.

The point P so obtained is the required point which divides AB internally in the ratio m:n.

question 1. To divide a line segment in a given ratio 3 : 2.

Solution: Given a line segment AB, we want to divide it in the ratio 3 : 2.

Steps of construction:

1. Draw any ray AX, making an acute angle with AB.

2. Locate 5(= m + n) points  A₁,A₂,A₃,A_4, and A₅ on AX so that

AA1 = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.

3. Join BA₅.

4. Through the point A₃ (m = 3), draw a line parallel to A₅B (by making an angle equal to ∠AA₅B) intersecting AB at the point C

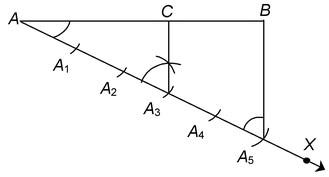
Then, AC : CB = 3 : 2

Let us see how this method gives us the required division.

Since A₃C is parallel to A₅B therefore,

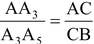(By the basic proportionality theorem)

By construction, 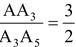Therefore, .

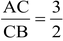This shows that C divides AB in the ratio 3 : 2

We now use the above ideas of construction for constructing a triangle similar to a given triangle above whose sides are in a given ratio with the corresponding sides of the given triangle.

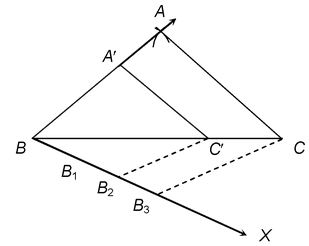
Question 2. Construct a triangle of sides 4 cm, 5 cm and 6 cm then construct a triangle similar to it whose sides are 2/3 of the corresponding sides of it.

Solution: Steps of construction:

1. Take BC = 6 cm. Let ∠CBX be any acute angle (< 90°).

2. Mark the three points B₁,B₂,B₃ (number of parts should be larger of the 2 and 3 in 2/3) such that BB₁ = B₁B₂ = B₂B_3.

3. Join B₃C and draw a line through B₂ (the second point) parallel to B₃C which meets BC at C′.

4. Draw C'A' parallel to CA which intersects AB at A′.

Do solve NCERT text book for class 10 maths with the help of Physics Wallah NCERT solutions for class 10 maths.