Alternative Method For Division Of A Line Segment Internally In A Given Ratio

Use the following steps to divide a given line segment AB internally in a given ration m : n, where m and natural members.

STEPS OF CONSTRUCTION:

(i) Draw a line segment AB of given length.

(ii) Draw any ray AX making an acute angle ∠BAX with AB.

(iii) Draw a ray BY, on opposite side of AX, parallel to AX making an angle ∠ABY equal to ∠BAX.

(iv) Mark off a points A₁, A_2,....Am’ on AX and n points B₁, B₂,...Bn on BY such that AA₁ = A₁A₂ = ...... = A_m-1 A_m = B₁B₂ = ....B_n-1B_n.

(v) Join A_mB_n. Suppose it intersect AB at P.

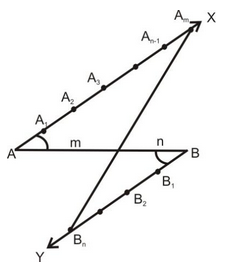
The point P is the required point dividing AB in the ratio m : n.

question 1. Decide a line segment of length 6 cm internally in the ratio 3:4.

Solution: Follow the following steps :

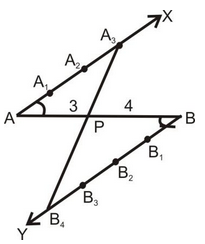
STEPS OF CONSTRUCTION:

(i) Draw a line segment AB of length 6 cm.

(ii) Draw any ray AX making an acute angle ∠BAX with AB.

(iii) Draw a ray BY parallel to AX by making ∠ABY equal to ∠BAX.

(iv) Mark of three point A₁,A₂,A₃ on AX and 4 points B1, B2m B3, B4 on BY such that AA₁ = A₁A₂ = A₂A₃ = BB₁ = B₁B₂ = B₂B₃ = B₂B₄.

(v) Join A₃B₄. Suppose it intersects AB at a point P.

Then, P is the point dividing AB internally in the ratio 3:4.