
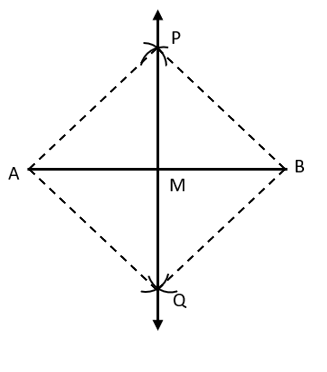
CBSE Class 9 Maths Notes Chapter 11: CBSE Class 9 Maths Notes Chapter 11 describes how to draw various forms with a ruler and compass. This chapter explains how to construct the bisector of a given angle and how to construct a perpendicular bisector of a given line segment.
Construction instructions and a clear illustration are provided. To get good grades, you should also complete all of the class 9 Maths Chapter 11 building problems in the textbook.CBSE Class 9 Maths Notes Chapter 11
The important topics and subtopics covered under Constructions class 9 are:
- Introduction
- Basic constructions
- Some constructions of triangles
- Summary
Linear Pair axiom
- The neighboring angles create a linear pair of angles if a ray is on a line.
- Uncommon arms of both angles make a straight line if two angles create a linear pair.
CBSE Class 9 Maths Notes Chapter 11 PDF
The foundation of the CBSE Class 9 Maths Notes Chapter 11 Constructions is the foundation for comprehending basic arithmetic ideas used in many different professions in geometry. Building geometric forms is a crucial ability that necessitates a thorough understanding of their characteristics. Students must therefore thoroughly study this subject. To learn more about this geometry topic, consult CBSE Class 9 Maths Notes Chapter 11 Constructions pdf. These answers serve as guidelines to motivate kids to learn. These notes extremely thorough content organization makes it simple and quick to pick up new concepts.CBSE Class 9 Maths Notes Chapter 11 PDF
Triangle Constructions
Construction of Triangles
To make a triangle, at least three elements must be provided; however, not every combination of three parts will work. Consequently, if the following triangle components are available, a unique triangle can be created:- There are two sides and an integrated angle.
- There are three sides provided.
- There are two angles and a given included side.
- A right triangle has one side and a hypotenuse.
- It is not always possible to build such a triangle uniquely given two sides and an angle (not the included angle).
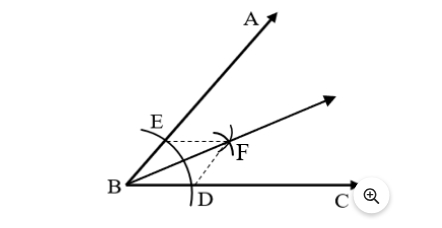
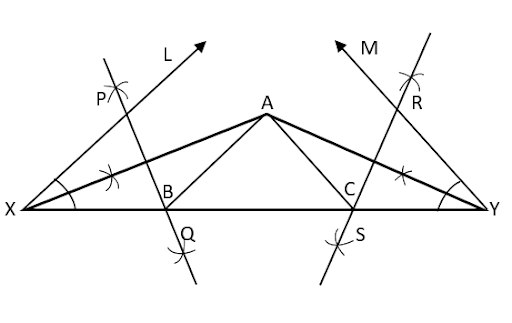
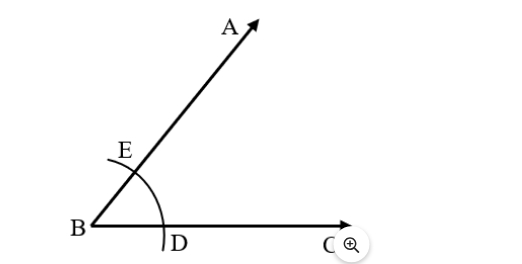 Create arcs with E and D as their centers and a radius greater than 1 by 2 DE so that they cross at F.
Create a ray that now connects B and F and extends it. Therefore, the necessary angle bisector is BF.
Create arcs with E and D as their centers and a radius greater than 1 by 2 DE so that they cross at F.
Create a ray that now connects B and F and extends it. Therefore, the necessary angle bisector is BF.

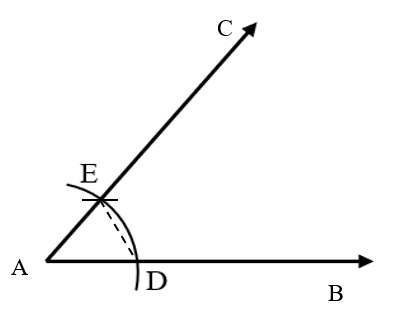
 To create a 60∘ angle at a given ray's starting point, take a ray AB with an initial point of A. From there, draw another ray AC so that ∠BAC=60∘. The actions that need to be taken are as follows:
Using A as the center, sketch an arc that intersects the ray AB at point D. Now, draw two arcs that intersect at a point, let's say E, using A and D as the centers and AD as the radius.
Connect AE and extend it to point C on the AC ray. Therefore, CAB=60∘.
To create a 60∘ angle at a given ray's starting point, take a ray AB with an initial point of A. From there, draw another ray AC so that ∠BAC=60∘. The actions that need to be taken are as follows:
Using A as the center, sketch an arc that intersects the ray AB at point D. Now, draw two arcs that intersect at a point, let's say E, using A and D as the centers and AD as the radius.
Connect AE and extend it to point C on the AC ray. Therefore, CAB=60∘.
Some Construction of Triangles:
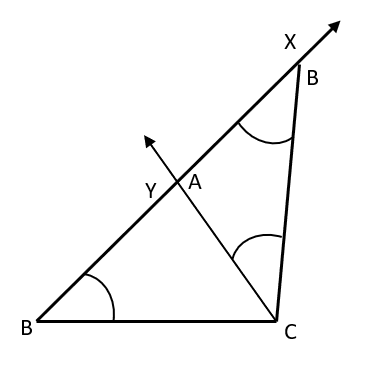
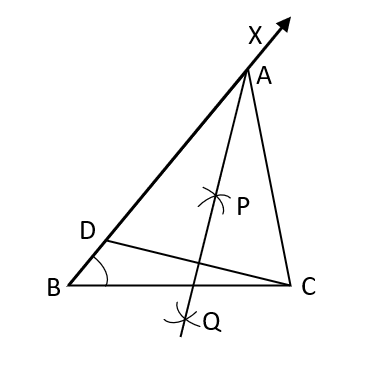
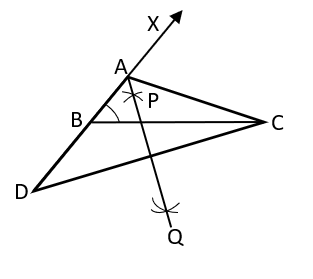
To create a triangle, measurements of at least three of its components are needed. However, none of the three-element combinations is sufficient for the goal. For instance, given the dimensions of the aspects and an uncovered perspective among the offered aspects, it is not possible to create a unique triangle. When (i) the base, one base attitude, and the total of the opposing aspects are provided, a triangle can be constructed. (ii) the basis, a foundational mindset, and the differentiation between the opposing elements are provided (iii) The base and perimeter angles are provided.


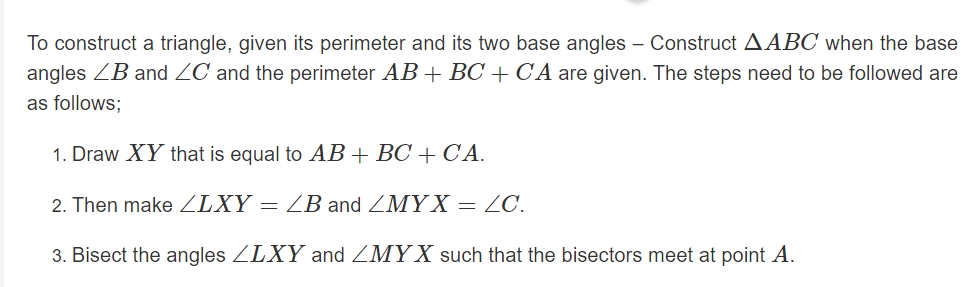

Benefits of CBSE Class 9 Maths Notes Chapter 11
Concept Clarity: CBSE Class 9 Maths Notes Chapter 11 helps students to understand the chapter better. Students can gain a firm grasp of these ideas.
Problem-solving abilities: The notes provide students with a range of practice problems and examples to aid in the development of their problem-solving abilities. Students can strengthen their grasp of ideas and develop their problem-solving skills by completing these notes.
Structured Learning: The notes are arranged methodically, covering subjects one after the other. This facilitates pupils' ability to learn logically.
Exam Preparation: CBSE Class 9 Maths Notes Chapter 11 is tailored to match the format of the exams. Students can improve their performance in the mathematics portion and successfully prepare for their exams by going over these notes.
CBSE Class 9 Maths Notes Chapter 11 FAQs
What is construction in math class 9?
Which is the hardest chapter in maths class 9?
Which is the most scoring chapter in class 9 maths?










