Equilibrium Constants Kc And Kp
Ionic And Chemical Equilibrium of Class 11
Equilibrium Constants Kc And Kp
(i) Let us consider a reaction of the type
A(g) + B(g)  C(g) + D(g). It is observed that for such an equilibrium, there exists an equilibrium constant, K, which is given as,
C(g) + D(g). It is observed that for such an equilibrium, there exists an equilibrium constant, K, which is given as,
K = 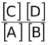
This implies that irrespective of the substance we start with (i.e. either A & B or C & D or A+B+C or A+B+D or A+C+D or B+C+D or A+B+C+D) and how much of these we start with, the ratio of 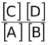 is a fixed quantity at a given temperature when the reaction reaches equilibrium. For instance, if we assume that the K = 10 for this equilibrium, then no matter what we take initially and irrespective of how much we take, once the equilibrium is established the ratio of
is a fixed quantity at a given temperature when the reaction reaches equilibrium. For instance, if we assume that the K = 10 for this equilibrium, then no matter what we take initially and irrespective of how much we take, once the equilibrium is established the ratio of 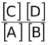 will always be equal to 10. This certainly looks surprising.
will always be equal to 10. This certainly looks surprising.
Well, the answer lies in the real understanding of the term equilibrium. At equilibrium the forward rate of reaction is equal to the reverse rate of reaction. That is,
rate of forward reaction = kf [A] [B] (where kf is the rate constant of forward reaction)
rate of reverse reaction = kr [C] [D] (where kr is the rate constant of reverse reaction )
At equilibrium,
∴ kf [A] [B] = kr [C] [D]
∴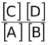
As kf and kr are the constants at a given temperature, thus their ratio (kf/kr) would also be constant. Therefore , the ratio of 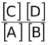 is also constant called Keq.
is also constant called Keq.
∴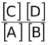
Since, this expression involves all variable terms, so the ratio of 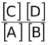 would also be constant called Kc. [When the ratio of concentration of reactants and products is taken into account, the equilibrium constant is called Kc]
would also be constant called Kc. [When the ratio of concentration of reactants and products is taken into account, the equilibrium constant is called Kc]
∴Kc = 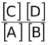
Assuming these gases to behave ideally, we can apply ideal gas equation
PV = nRT
P =  = CRT
= CRT
C = 
∴[C] =  , [D] =
, [D] =  , [A] =
, [A] =  , [B] =
, [B] = 
∴Kc = 
where  and PB are the partial pressures of C, D, A and B respectively.
and PB are the partial pressures of C, D, A and B respectively.
Since LHS is a constant, thus the ratio of partial pressures of products to reactants would also be a constant called Kp.
∴Kp = 
For this equilibrium, Kp = Kc but for other equilibria, this may not be the case.
(ii) Now, let us consider the reaction of the type
A(s) + B(g)  C(soln.) + D(g)
C(soln.) + D(g)
Its equilibrium constant , Keq would be
Keq = 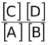
Concentration of C is the number of moles of C per unit volume of solution. Concentration of D is the number of moles of D per unit volume of the container (we can assume that volume of the solution is negligibly small in comparison to the volume of container and thus the volume occupied by the gas is equal to the volume of the container). The concentration of A is the number of moles of A per unit volume of solid, A. The concentration of all pure solids and pure liquids is a constant. This is because if initially we take w gm of A, then the moles of A are w/M. The volume of A is w/d where d is the density of A. Therefore, the initial concentration of A is  . Thus, it is evident that at equilibrium also the concentration of A remains as d/M ( d and M are constants). In fact even if A were a pure liquid, its concentration would have remained constant.
. Thus, it is evident that at equilibrium also the concentration of A remains as d/M ( d and M are constants). In fact even if A were a pure liquid, its concentration would have remained constant.
So, here the concentration of A does not change with time while the concentration of B, C and D varies with time.
Therefore, we bring all the constant terms on one side and we get
Keq[A] =
This ratio which is a constant and which involves only those concentration terms which are variables is called Kc.
∴KC =  = Keq [A]
= Keq [A]
[Note: The distinction between Kc and Keq is that in the expression of Keq all the substances are involved while in the expression of Kc only solutions and gases are involved. The expression of Kc is devoid of pure components like pure solids & pure liquids as their concentrations are constant]
(iii) Let us consider another reversible reaction of the type
x1A(g) + x2B(g)  y1C(g) + y2D(g)
y1C(g) + y2D(g)
The expression of equilibrium constant would be
∴Keq = 
Since in this expression all the terms are variables, so the ratio of  would also be constant called Kc.
would also be constant called Kc.
∴Kc = 
As we know, the concentration of a gas is given by P/RT. Thus,
[C] =  , [D] =
, [D] =  , [A] =
, [A] =  , [B] =
, [B] = 
∴Kc = 
∴Kc 
LHS of this equation being a constant since T is fixed and R and Kc are constants. Thus, RHS of the equation would also be constant. Therefore, for this equilibrium the ratio of partial pressures raised to the power of proper stoichiometric coefficients is also a constant called Kp.
∴Kp =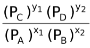
Now let us assume that A is either pure solid or pure liquid. For such equilibrium, the expression of Kc would be
Kc =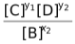
and following the above given sequence of derivation, Kp would be
Kp =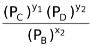
Now if we assume that A was a solute present in a solution then the expression of Kc would remain the same i.e, Kc = 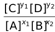 . Now if we try to express the concentrations in terms of partial pressures, we would fail to do that for A as it is not possible to express the concentration of a solution in terms of its pressure or vapour pressure and constants.
. Now if we try to express the concentrations in terms of partial pressures, we would fail to do that for A as it is not possible to express the concentration of a solution in terms of its pressure or vapour pressure and constants.
Therefore [A] remains as such
∴KC = 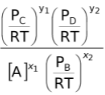

The R.H.S. of the above expression is a constant which implies that the L.H.S is also a constant. This new expression cannot be called as either KC or KP since it contains both concentration terms and pressure terms. We call it KPC. We can also see that if we take [A] to the R.H.S. the L.H.S. contains only pressure terms, but then it is not a constant since [A] is a variable.
Therefore, we can conclude that Kp exists for those equilibria which fulfill the given conditions.
(i) It must have atleast one gas either in the reactants or in the products and
(ii) it must not have any component in solution phase.
Relation Between Kp And Kc
In general, relation between Kp and Kc for a reversible reaction Kp = 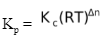
where Δn = number of moles of gaseous products - number of moles of gaseous reactants
R = Gas constant
and T = Absolute temperature
[Remember that value of R is to be used in the units of litre atm per mole per Kelvin].
(i)If Δn = 0, then Kp = Kc, For example N2(g) + O2(g)  2NO(g)
2NO(g)
(ii)If Δn > 0, then Kp > Kc,
For example PCl5(g)  PCl3(g) + Cl2(g), where Δn = 2 − 1 =1
PCl3(g) + Cl2(g), where Δn = 2 − 1 =1
(iii) If Δn < 0, then Kc > Kp,
For example N2(g) + 3H2)(g) 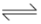 2NH2(g), where Δn = 2 − 4= −2
2NH2(g), where Δn = 2 − 4= −2
Units of Kp and Kc
When the concentration of species are expressed in moles per litre, then the unit of Kc
would be  . Similarly, when the pressure is expressed in atmospheres, the unit of
. Similarly, when the pressure is expressed in atmospheres, the unit of
Kp would be  .
.
[Note: The unit of Kp or Kc given for an equilibrium in a problem signifies that whether the value of equilibrium constant is given for equilibrium in forward direction or in reverse direction].
- Equilibrium
- Equilibrium Constants Kc And Kp
- Factors Affecting Equilibrium Constant
- Eqilibrium Constants For Different Types Of Equilibria
- Reaction Quotient Prediction Of Direction Of Reaction
- Le Chateliers Principle
- Relation Between Degree Of Dissociation And Vapour Density
- Free Energy Change And Spontaneity Of A Reaction
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6









