What is ANGLE

Intersecting Lines

Tow lines are intersecting if they have a common point. The common point is called the ‘Point of intersection’.

Parallel Lines

Two lines are said to be parallel lines if they do not have a common point i.e., they do not intersect anywhere. If two lines I and m are parallel then they are represented as I || m.

Theorem 1 : Two distinct lines have only one point in common.

Given : Two distinct line I and m.

To Prove : Line I and m have atmost one point in common

Proof : Let lines I and m have two points P and Q in common. Then I contains the points P and Q and also line m contains the points P and Q. But there is one and only one line passing through two distinct points. Therefore I and m are identical. This contradicts the our assumption that two lines are distinct lines. Hence two distinct lines cannot have more than one point in common.

Theorem 2 : Two lines which are both parallel to the one line are parallel to each other.

Given : Three lines I, m and n in a plane such that I parallel to m and I || n.

To Prove : m || n.

Proof : Let m is not parallel to n. Then m and n intersect at a point. Thus through a point outside I, there are two lines m and n both parallel to I. This is not possible so our assumption is wrong. So m || n.

Theorem 3 : If I, m and n are three lines in a plane where I intersects m and m is parallel to n, then I also intersect n.

Given : Three lines I, m and n in the plane such that I intersect m and m || n.

To Prove : I intersect n.

Proof : Let I does not intersect n. Then I || n but m || n

I || m 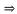I and m are non-intersecting lines.

This is a contradiction. So I intersect n.

Theorem 4 : If I and m are intersecting lines I || p and m || q, then p and q also intersect.

Given : Four lines I, m, p and q such that I || p, m || q and I and m intersecting.

To Prove : Lines p and q intersect.

Proof : If I and m are intersecting and I || p, then m and p are intersecting liens. Now m II q therefore p and q intersect.

Line Segments :

Given two points A and B on a line I the continuous part of the line with and points A and B is called the line segment AB.

Distance between two Points :

The distance between two points A and B is the length of the line segment joining them and is denoted by AB.

Example 3 : If A, B and C are three points on a line and B lies between A and C, then prove that
AB + BC = AC.

Solution : From the given figure AC coincides with AB + BC. Also, things which coincide with one another are equal to one another

AC = AB + BC.

Ray : Let a line I and two distinct points A and B on I. Now consider the part of I which has only one end point at A and contains the point B. This part of line I is called a ray.

SOME IMPORTANT DEFINITIONS

(i) Collinear points :Three or more points are said to be collinear if there is a line which contains all of them.

(ii) Concurrent Lines : Three or more lines are said to be concurrent if there is a point which lies on all of them.

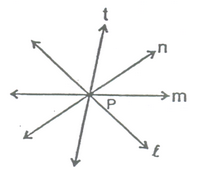
 (iii) Intersecting lines :Two lines are intersecting if they have a common point. The common point is called the “point of intersection”.

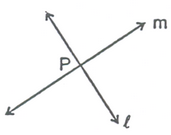
(iv) Parallel lines : Two lines I and m in a plane are said to be parallel lines if they do not have a common point.

(v) Line Segment :Given two points A and B on a line I, the connected part (segment) of the line with end points at A and B, is called the line segment AB.

(vi) Interior point of a line segment :A point R is called an interior point of a line segment PQ if R lies between P and Q but R is neither P nor Q.

(vii) Congruence of line segment :Two line segments AB and CD are congruent if trace copy of one can be superposed on the other so as to cover it completely and exactly in this case we write AB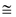CD. In other words we can say two lines are congruent if their lengths is same.

(viii) Distance between two points :The distance between two points P and Q is the length of line segment PQ

(ix) Ray :Directed line segment is called a ray. If AB is a ray then it is denoted by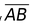. Point A is called initial point of ray.

(x) Opposite rays :Two rays AB and AC are said to be opposite rays if they are collinear and point A is the only common point of the two rays.

EQUIVALENT VERSIONS OF EUCLID’S FIFTH POSTULATE

There are several equivalent versions of the fifth postulate of Euclid. One such version is stated as ‘Playfair’sAxiom’ which is given below:

 

PLAYFAIR’S AXIOM (AXIOM FOR PARALLEL LINES):

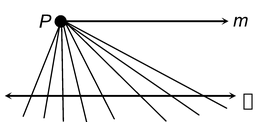
For every line λ and for every point P not lying on , there exists a unique line m passing through P and parallel to .

Let us observe it in figure.

Another version of the above axiom is as stated below:

Two distinct intersecting lines cannot be parallel to the same line.

In figure, there are infinitely many straight lines through P but there is exactly one line m which is parallel to . Thus, two intersecting lines cannot be parallel to the same line.

A STATEMENT AS A THEOREM:

Euclid deduced 465 geometrical properties by using definitions, axioms and postulates. These properties are called theorems.

The properties confirmed through logical reasoning based on some axioms, postulates and previously proved results are called theorems or propositions. 

Two distinct lines cannot have more than one point in common.

Let us suppose that the two lines intersect in two distinct points, say P and Q. So, we have two lines passing through two distinct points P and Q. But this assumption contradicts with the axiom that only one line can pass through two distinct points. Hence our assumption is wrong. Thus we conclude that two distinct lines cannot have more than one point in common.

A CONSISTENT COLLECTION OF AXIOMS:

A collection of axioms is consistent, if it is impossible to derive from these axioms a result that contradicts any axiom or postulate or previously proved property.

All the attempts to prove Euclid’s fifth postulate using the first 4 postulates failed. But they led to the discovery of several other geometries, called non-Euclidean geometries.

1. If a point C lies between two points A and B such that AC = BC, then prove that AC = 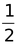AB. Explain by drawing the figure.

Solution: According to the given statement, the figure will be as shown alongside in which the point C lies between two points A and B such that AC = BC.

2. Give a definition for each of the following terms. Are there other terms that need to be defined first ? What are they, and how might you define them ?

(i) parallel lines (i) perpendicular lines (iii) line segment (iv) radius

Solution: (i) Parallel lines : Lines which don’t intersect anywhere are called parallel lines.

(ii) Perpendicular lines :Two lines which are at a right angle to each other are called perpendicular lines.

(iii) Line segment :It is a terminated line.

(iv) Radius :The length of the line-segment joining the centre of a circle to any point on its circumference is called its radius.

3. How would you rewrite Euclid’ fifth postulate so that it would be easier to understand?

Solution: Two distinct intersecting lines cannot be parallel to the same line.

4. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.

Solution: If a straight line falls on two straight lines m and n such that sum of the interior angles on one side of is two right angles, then by Euclid’s fifth postulate the line will not meet on this side of. Next, we know that the sum of the interior angles on the other side of line also be two right angles. Therefore they will not meet on the other side. So, the lines m and n never meet and are, therefore parallel.

THEOREM 1:

If , m, n are lines in the same plane such that intersects m and n ║ m, then intersects n also. 

Given: Three lines , m, n in the same plane such that intersects m and n ║ m.

To prove: Lines and n are intersecting lines.

.

This is a contradiction to the hypothesis that and m are intersecting lines.

So our supposition is wrong.

Hence, intersects line n.

THEOREM 2:

If lines AB, AC, AD and AE are parallel to a line , then points A, B, C, D and E are collinear.

Given: Lines AB, AC, AD and AE are parallel to a line .

To prove :A, B, C, D, E are collinear.

Proof: Since AB, AC, AD and AE are all parallel to a line Therefore point A is outside and lines AB, AC, AD, AE are drawn through A and each line is parallel to .

But by parallel lines axiom, one and only one line can be drawn through the point A outside it and parallel to .

This is possible only when A, B, C, D, and E all lie on the same line. Hence, A, B, C, D and E are collinear.