What is LINE
Lines and angles of Class 9
The word ‘geometry’ is derived from the Greek words ‘geo’ meaning ‘earth’ and ‘metron’ meaning ‘measuring’. Thus the word ‘geometry’ means the measurement of earth. Firstly ancient Egyptians developed a number of geometric techniques and rules for calculating simple areas and also for doing simple constructions. They were mainly concerned with problems of finding the areas of plane figures such as triangles, rectangles etc.
Firstly, geometry is used by Egyptians and they passes these knowledge to Greek people. Thale and his pupil Pythagoras were the Greek mathematician who worked on geometry. Euclid was the first Greek mathematician who initiated a new way of thinking the study of geometry. He introduced the method of proving a geometrical result by the use of already proved results.
Axioms (Postulates) and Theorems
Axioms : The basic facts which are taken for granted, without proof are called axioms.
Illustration 1 : A point is that which has no part.
Illustration 2 : If a < b, b < c then a < c
Theorems : the conclusions obtained through logical reasoning based on previously proved results and some axioms is known as a theorem or a proposition.
There are three basic terms in geometry known as ‘Point’, ‘Line’ and ‘Plane’. It is not possible to define these three terms precisely.
EUCLID’S DEFINITIONS
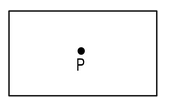
Points : A point is that which has no part.
Line : A line is breathless length.

Surface : A surface is that which has length and breadth only.
Ends of a line : The ends of a line are points.
Edges of a Surface : The edges of a surface are lines.
Straight line : A straight line is a line which lies evenly with the points on itself.
Plane Surface : A plane surface is a surface which lies evenly with the straight lines on itself.
EUCLID’S AXIOMS:
Axioms :The assumptions, used throughout in mathematics which are obvious universal truths, are termed as axioms.
Axioms given by Euclid are as under :
1. Things which are equal to the same thing are equal to one another.
i.e., if a = c and b = c, then a = b.
For example, if area of a circle is equal to that of square and the area of the square is equal to that of a rectangle, then the area of the circle is equal to the area of the rectangle.
Things to remember
-
The magnitudes of only same kind of things can be compared.
-
The length of a line may be equal to the area of a circle in magnitude but the two cannot be compared with each other.
-
If equals are added to equals, the wholes are equal. i.e., if a = b and c = d, then a + c = b + d.
Also a = b⇒a + c = b + d.
Here, a, b, c and d are same kind of things.
- If equal are subtracted from equals, the remainders are equal.
- The things which coincide with one another are equal.
- The whole is greater than the part.
i.e. if a>b, then there exists c such that a = b + c.
Here, b is a part of a and therefore, a is greater than b.
- Things which are double of the same things are equal to one another.
- Things which are halves of the same things are equal to one another.
EUCLID’S POSTULATES:
Postulates : The assumptions, specific to geometry which are obvious universal truths, are termed as postulates. Euclid gave five postulates as stated below :
Postulate 1 :A straight line may be drawn from any one point to any other point.
Postulate 2 : A terminated line (i.e., a line segment) can be produced indefinitely on either side.
Postulate 3 :A circle can be drawn with any centre and any radius.
Postulate 4 :All right angles are equal to one another.
Postulate 5 :If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.
INCIDENCE AXIOMS:
Axiom 1 : A line contains infinitely many points.
Axiom 2 : Through a given point, infinitely many lines passes.
Axiom 3 : From given two points A and B. One and only one line can be drawn. Given figure represents a line

Collinear Points
Three or more points are said to be collinear if there is a line which contains all of them.
Concurrent Lines
Three or more lines are said to be concurrent if there is a point which lies on all of them.









