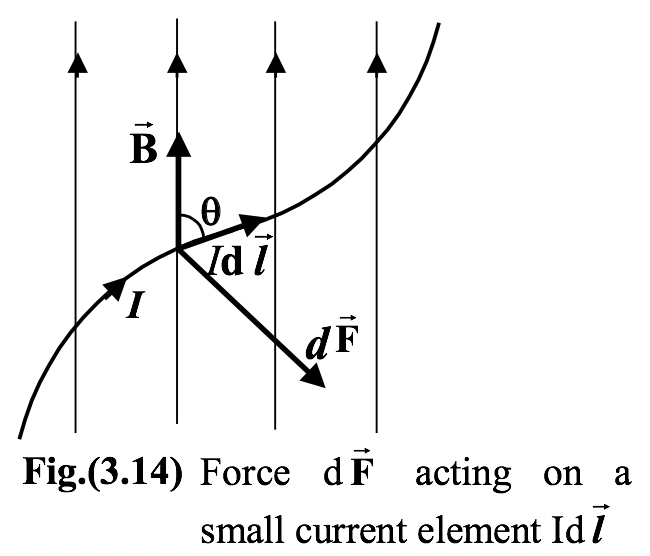
Force On A Current Carrying Conductor
Magnetics of Class 12
When a wire is placed in a magnetic field, it experiences no force. The thermal velocities of the free electrons are randomly oriented and so net force on them is zero. However, when a current flows, the electrons as a whole acquire a velocity in a definite direction and experience a magnetic force which is then transmitted to the wire.
|
The force experienced by an infinitesimal current element Id
d The total force on a wire is the vector sum (integral) of the forces on all current elements.
∫d |
|
Example: 3.10
|
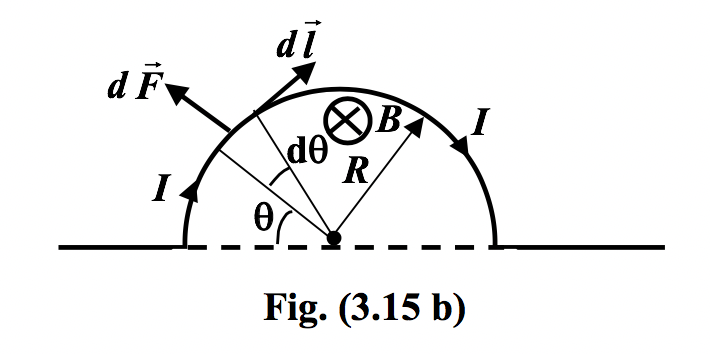
A wire is bent into a semi-circular loop of radius R. It carries a current I, and its plane is perpendicular to a uniform magnetic field B, as shown in Find the force on the loop. |
|
Solution
Consider a small element dl at an angle θ as shown in fig. (3.15 a).
The magnitude of force is dF = I dl B sin90° = IB dl = IBR θ
The force can be resolved into components
|
dFx = dF cos θ = IBR cos θ dθ (i) dFy = dF sin θ = IBR sin θ dθ (ii) On integrating (i) and (ii) , we get
Fx = IBR
Fy = IBR |
|
Note that it is equal to the force acting on a straight wire of length 2R.
IMPORTANT
If the magnetic field is uniform and the current is constant, then both can be removed from the integral :
|
∫d
here ∫d The force on a curved wire joining point 1 and 2 is the same as that on a straight wire joining these points, as shown in fig (3.16). |
|
Force of Interaction Between Parallel Wires
The interaction between two parallel wires can be summarised as follows :
1. Like currents attract while unlike currents repel each other.
2. The force of interaction per unit length is proportional to the product of the currents in each wire.
3. The force is inversely proportional to the distance between them.
Consider two very long parallel wires carrying current I1 and I2 in the same direction as shown in the figure (3.17). The magnetic field produced by the current I1 at the position of I2 is given by
B21 = 
Note that the direction of 
21 is perpendicular to wire 2. So the magnitude of force on wire 2 is
21 = I2 (d
× 21) ⇒ F21 = I2 l B21 sin90°
or F21 = I2l
or F21 = 
By applying the right hand rule one can note that the force is toward wire 1. The same analysis can be performed to find the force on the wire 1.
Thus, the force of interaction per unit length between two parallel wires is
(3.18)
|
Example: 3.11
A rectangular loop of length l and width b carrying a current I2 is placed in the neighbourhood of a long strength wire carrying current I1 and shown in (a) Find the net force acting on the loop (b) Find the work done to increase the spacing between the loop and the wire from a to 2a. |
|
|
Solution
(a) The force acting on each side of the loop are shown in
F1 =
F2 = The net force on the loop is horizontal and it is attractive.
Fnet = F1 − F2 = |
|
(b) If F is the instantaneous force acting on the loop when its separation form the wire is x, then the work down to increase the spacing from a to 2a is
W = 
where F = 
Thus, W = 
