Magnetic Force
Magnetics of Class 12
The force due to magnetic field acts on electric charges in a particular manner. If you simply place an electric charge in a magnetic field nothing happens, i.e., when an electric charge is at rest in a constant magnetic field it experiences no magnetic force. Electric charges have to move to experience a force from a magnetic field.
IMPORTANT
1. The force on a charge q is proportional to the magnitude of the charge and its speed v. When the charge is not moving, there is no magnetic force on it.
2. The direction of the force is perpendicular to the direction of both the velocity v and the magnetic induction field B.
3. When the velocity of the charge is parallel to the magnetic field the force is zero.
F = |![]() | = qvB sin0 = 0
| = qvB sin0 = 0
The above points may be summarised in a mathematical expression as
F = q(![]() ×
× ![]() ) (3.10)
) (3.10)
The magnitude of the force is given by F = qvB sinθ
where θ is the angle between the vectors v and B.

Work done by a Magnetic Force is zero.
Since ![]() is always perpendicular to
is always perpendicular to ![]() there is no component of acceleration in the direction of velocity vector, therefore, magnitude of the velocity does not change, thus kinetic energy of the charge does not change, hence no work is done by the magnetic force.
there is no component of acceleration in the direction of velocity vector, therefore, magnitude of the velocity does not change, thus kinetic energy of the charge does not change, hence no work is done by the magnetic force.
|
Mathematically, it can be proved like this
W = ∫
=
Since d
Therefore W = q |
|
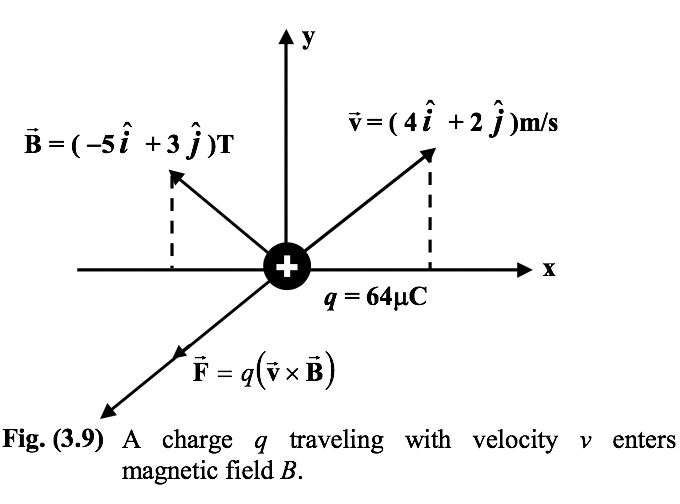
Example: 3.5
A 64μC charge travelling with velocity ![]() =
=  m/s enters a region where there is a magnetic field
m/s enters a region where there is a magnetic field ![]() =
=  T. Compute the force on the charge.
T. Compute the force on the charge.
Solution
|
The vectors
= (64 × 10−6) [12 + 10)
= 1.41 × 10−3 |
|
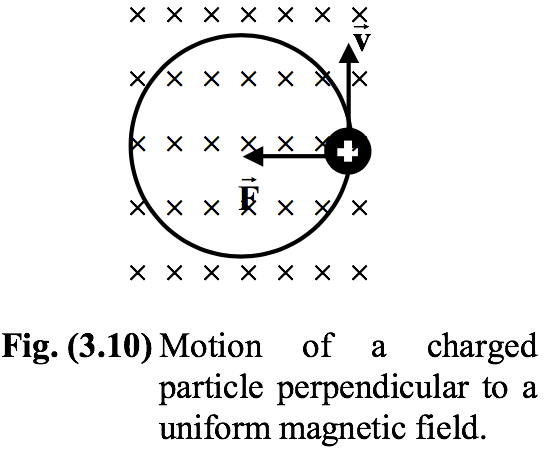
Motion of a charged particle in a Uniform Magnetic Field
|
Consider the motion of a positively charged particle moving with an initial velocity Under the action of such a force the particle moves in a circular path with constant speed. The magnetic force provides the centripetal force. Applying Newton’s second law qvB = mv2/r where r is the radius of the circular path. |
|
r = mv/qB (3.11)
The radius of the orbit is directly proportional to the linear momentum of the particle and inversely proportional to the magnetic field strength.
The time period is given by
T = 2πr/v = 2πm/qB(3.12)
Note that time period is independent of velocity. All particles with same charge to mass ratio (q/m), have the same period.
Example : 3.6
An electron with a kinetic energy of 103 eV moves perpendicular to the direction of uniform field B = 10−4 T.
(a) What is the period of its orbit ?
(b) What is the radius of the body ?
Solution
(a) Using equation (3.12)
T =  or T = 3.6 × 10-7s
or T = 3.6 × 10-7s
(b) Using equation (3.11), the radius of the orbit is given by
r = mv/eB
The momentum of the electron can be obtained from kinetic energy as
mv =  = 1.7 × 10−23 kg m/s
= 1.7 × 10−23 kg m/s
Thus, radius of the orbit is given by
r =  = 1.07 m
= 1.07 m
|
Example: 3.7 A particle of mass m and charge q is projected into a region having a perpendicular uniform magnetic field B. Find the angle of deviation θ of the particle as it comes out of the magnetic field if width d of the region is equal to (a) mv/2qB (b) mv/qB (c) 2mv/qB |
|
|
Solution (a) The radius of the circular orbit is given by r = mv/qB The angle of deviation is given by sinθ
= d/r = or θ = sin−1 1/2 = π/6 |
|
(b) When d = mv/qB = r, the charged particle deviates through an angle of π/2 as shown
in the Fig.(3.11 c), hence θ = π/2
|
|
|
(c)When d = 2 mv/qB= 2r, the charged particle completes one semi-circle and deviates through π, as shown in the Fig.(3.11 d), hence θ = π
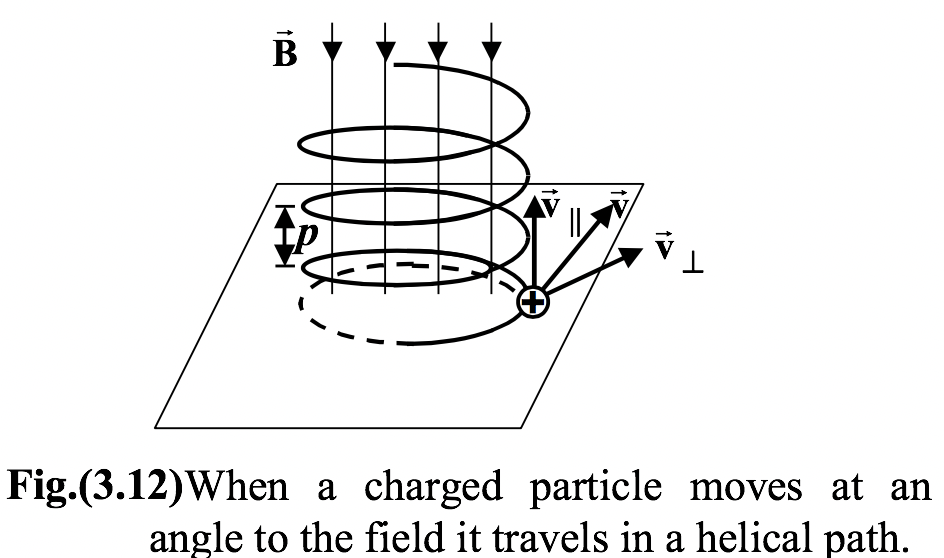
Helical Motion
|
Let us consider the motion of a positive charged particle whose velocity
|
|
The parallel component v|| is unaffected by the magnetic field ![]() , therefore, the particle moves with constant velocity parallel to the field. The resultant motion is a uniform circular motion perpendicular to field lines and a constant linear motion along the field lines. This is called a circular helical path.
, therefore, the particle moves with constant velocity parallel to the field. The resultant motion is a uniform circular motion perpendicular to field lines and a constant linear motion along the field lines. This is called a circular helical path.
Radius of helix r = mv⊥/qB (3.13)
The pitch of a helix is defined as the linear distance moved by the particle in one revolution.
p = v|| T = 2πmv||/qB (3.14)
Example: 3.8
An electron moving at 4 × 106 m/s enters a uniform field B = 0.04 T at 30° to the lines. What is the pitch of the helical path.
Solution
v|| = v cosθ
where v = 4 × 106 m/s ; = 30°
∴ v|| = (4 × 106) cos30° = 3.46 × 106 m/s
Using equation
p = 2πmv||/qB
or p = 2π = 3.1 mm
= 3.1 mm
Lorentz Force
When a particle is subjected to both electric and magnetic fields in the same region, the total force on it is called the Lorentz force.
![]() = q (
= q (![]() +
+ ![]() ×
× ![]() ) (3.15)
) (3.15)
We know that the path of particle in a uniform magnetic field is a helix and the path in a uniform electric field is parabola. When a particle is subject to both electric and magnetic fields, the motion is in general quite complex. However, the special cases in which the fields are either parallel to perpendicular to each other are simple to analyze.
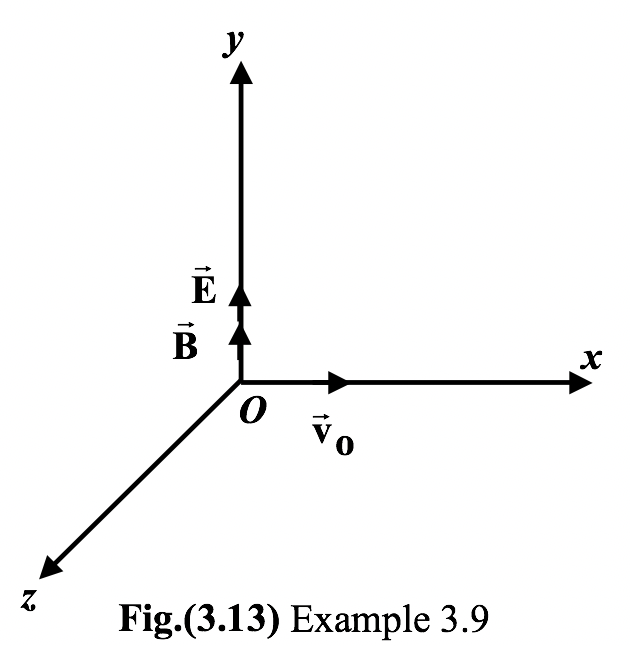
Example: 3.9
|
Uniform electric (a) Find the coordinate yn of the particle when it crosses the y-axis for the nth time. (b) Find the angle between the particle vector and the y-axis at that moment. |
|
Solution
(a) Since magnetic field does not accelerate a particle in its own direction, therefore, the distance moved along the y-axis is only due to electric field.
ay = qE/m
The period T = 2πm/qB
The time taken for n revolution is t = nT = 2πnm/qB
The distance travelled along the y-axis is
yn = 1/2 ayt2 = 1/2 (qE/m)(2πnm/qB)2
(b) The velocity parallel to the y-axis after time t
v|| = ayt = qEt/m = 2πnE/B
Velocity v⊥ to the y-axis is
v⊥ = vo
Now, tan θ = v⊥/v|| = v0B/2πnE
or θ = tan−1 (v0B/2πnE)
 q(
q(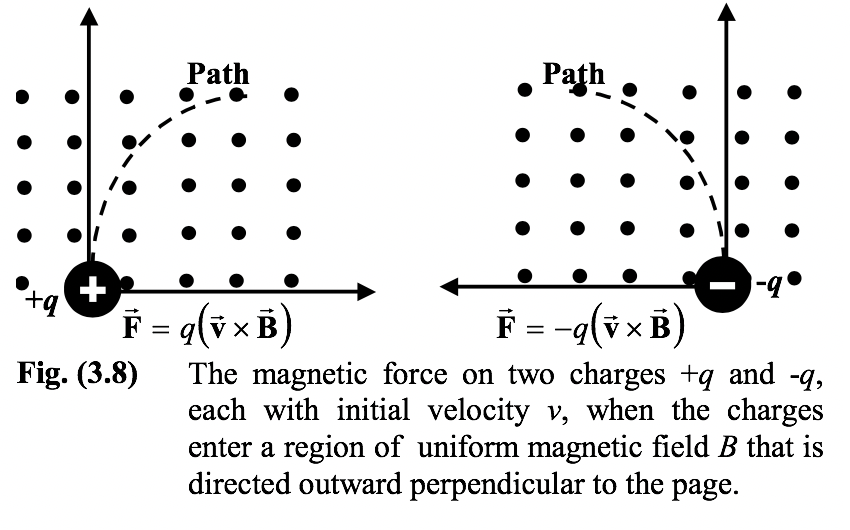

 ]
]