SPECIAL CASES QUADRILTERALS
Practical geometry of Class 8
CONSTRUCTING A QUADRILATERAL WHEN FOUR SIDES AND A DIAGONAL OF A QUADRILATERAL ARE GIVEN:
We consider the quadrilateral ABCD as a figure made of two triangles:
- ΔABC and ΔADC when diagonal AC as the common side is given.
- ΔABD and ΔBCD when diagonal BD as the common side is given.
In order to draw the quadrilateral when four sides and one diagonal are given, we first draw a rough sketch of the quadrilateral and write its dimensions along the sides and then we divide it into two triangles which can be drawn conveniently.
STEPS:
Step 1: Construct a triangle ABD (say).
Step 2: Find point C opposite to the vertex A as follows. With B as the centre and given radius, draw an arc on the other side of BD. Similarly with D as the centre and given radius, draw another arc intersecting the previous arc. The point of intersection of these arcs is marked as C.
Step 3: join points B and C, and D and C.
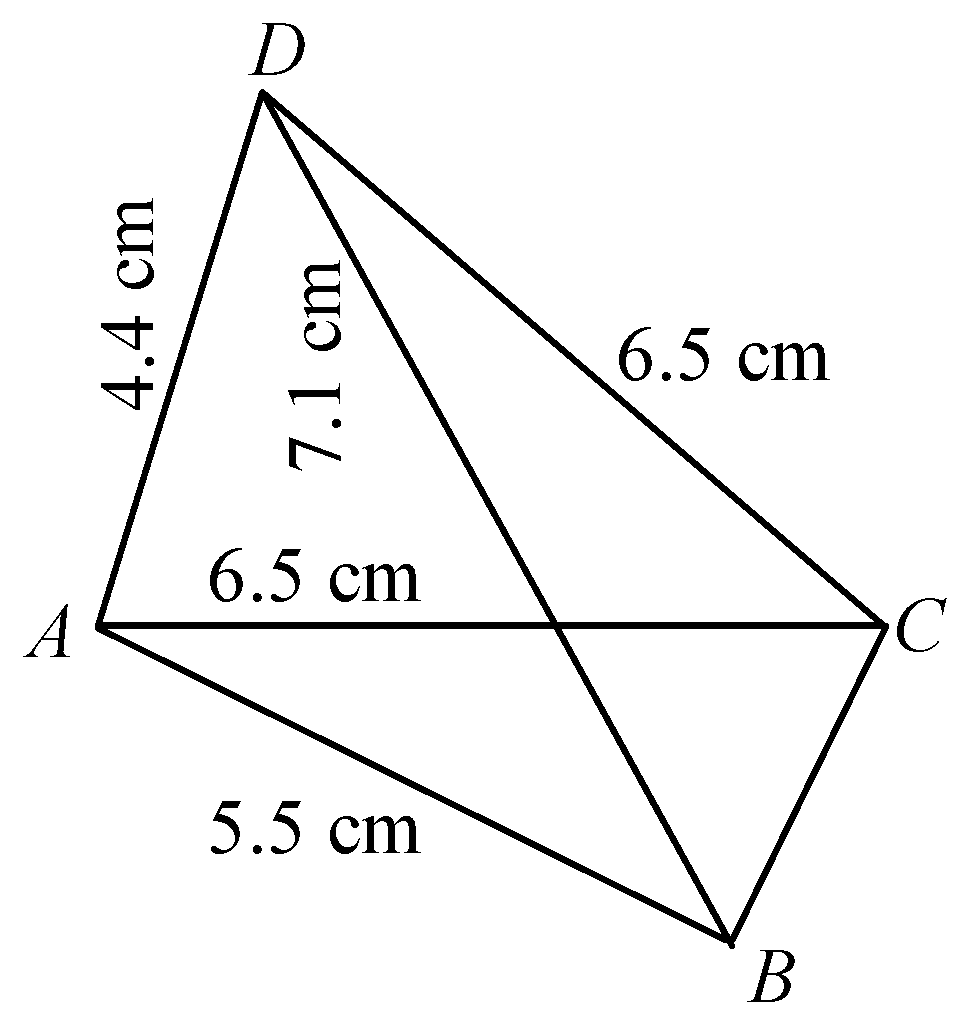
question 1. Construct a quadrilateral ABCD, in which AB = 5.5 cm, AD = 4.4 cm, CD = 6.5 cm, and AC = 6.5 cm and BD = 7.1 cm.
Solution: First we draw a rough sketch of quadrilateral ABCD. It is evident from the rough sketch that we have sufficient data to draw triangles ADC and ABD.
|
|
- Join AD, CD, AB and CB to obtain the required quadrilateral.
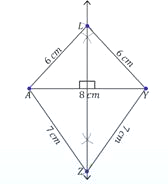
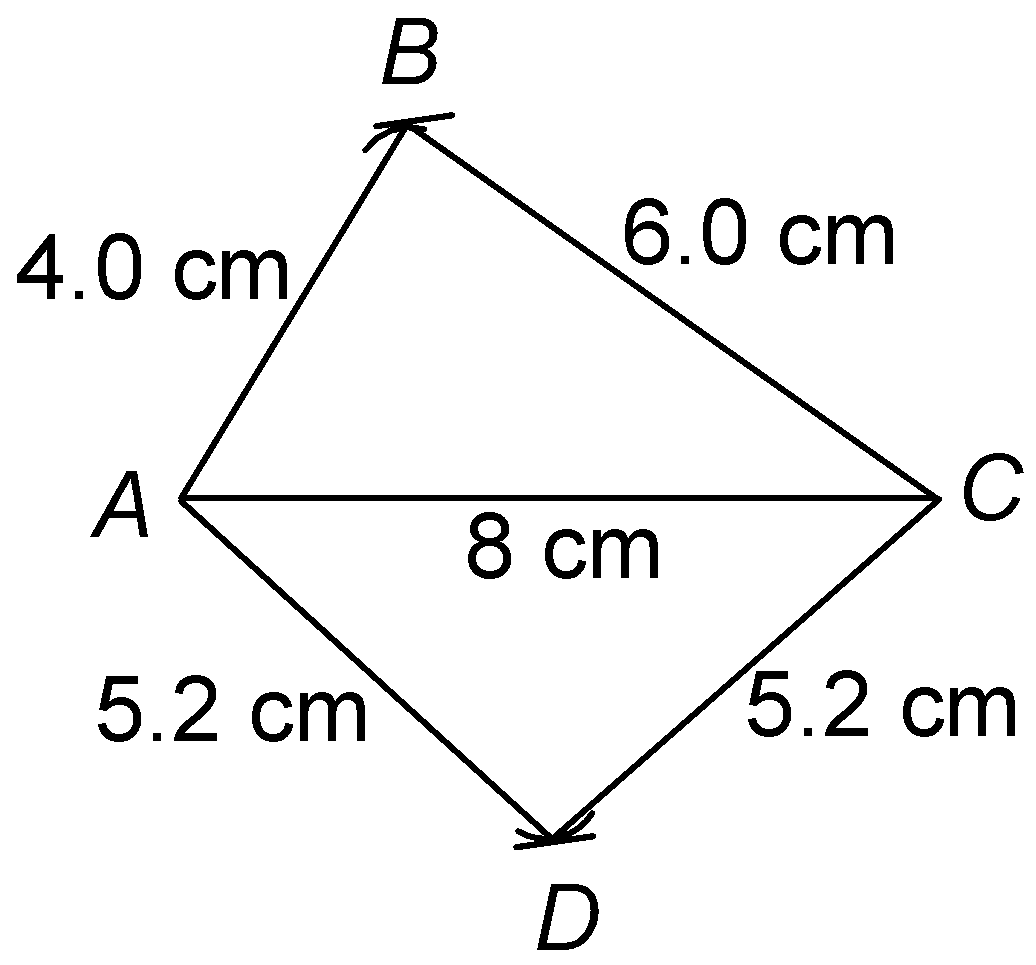
question 2. Construct a quadrilateral ABCD, when AB = 4 cm, BC = 6.0 cm, CD = DA = 5.2 cm and AC = 8 cm.
Sol. (i) Construct AC = 8 cm as shown in figure.
|
|
Thus, ABCD is the required quadrilateral.
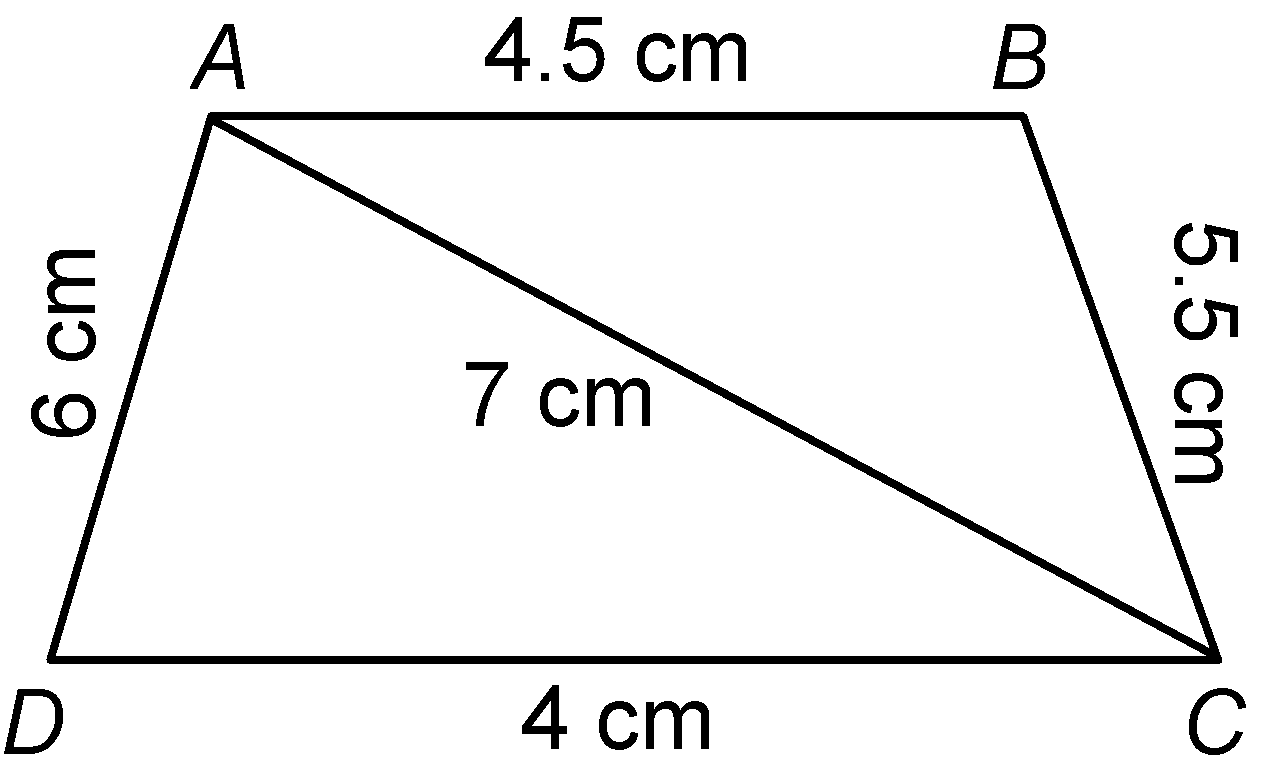
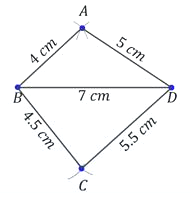
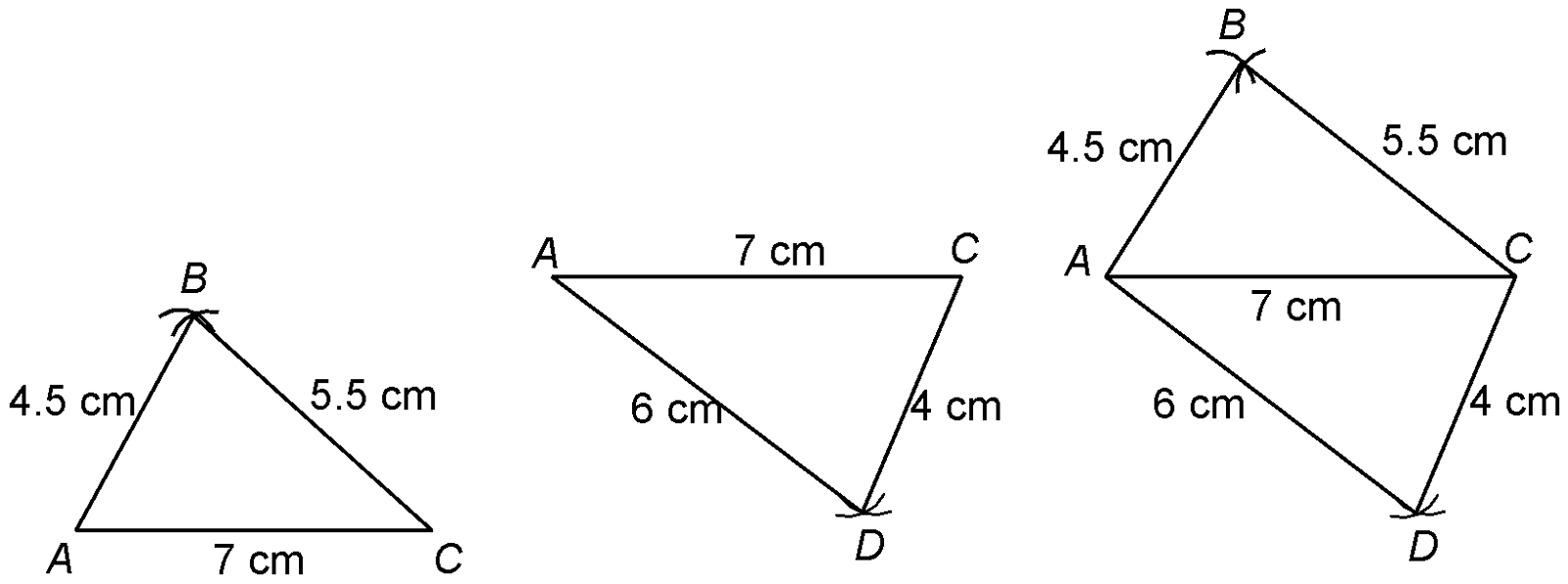
question 3. Construct the quadrilateral ABCD in which AB = 4.5 cm, BC = 5.5 cm, CD = 4, cm, AD = 6 cm and AC = 7 cm.
|
Solution: Steps of construction
|
|
- Repeat the construction to obtain ΔADC taking AD = 6 cm and DC = 4 cm.
- ABCD is the required quadrilateral
question 4. Construct the quadrilateral JUMP in which JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm and PU = 4 cm.
|
Solution: Steps of construction
|
|
question 5. Construct a parallelogram ABCD in which, AB = 6 cm, BC = 4.5 cm and diagonal AC = 6.8 cm.
|
Solution: Steps of construction
|
|
- Join BC and AC.
- With A as centre and radius 4.5 draw an arc.
- With C as centre and radius 6 cm draw another arc so as it cuts the previously drawn arc of step (v) at D.
- Join DA and DC.
Then, ABCD is the required parallelogram.
CONSTRUCTING A QUADRILATERAL WHEN LENGTHS OF ITS THREE SIDES AND TWO INCLUDED ANGLES:
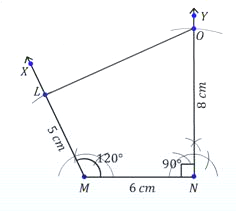
STEPS:
Step 1: Draw a line segment MN (say) of given length.
Step 2: Construct a given angle at M.
Step 3: Construct an angle 90° at N.
Step 4: Locate vertices L and O.
Step 5: Join L and O.
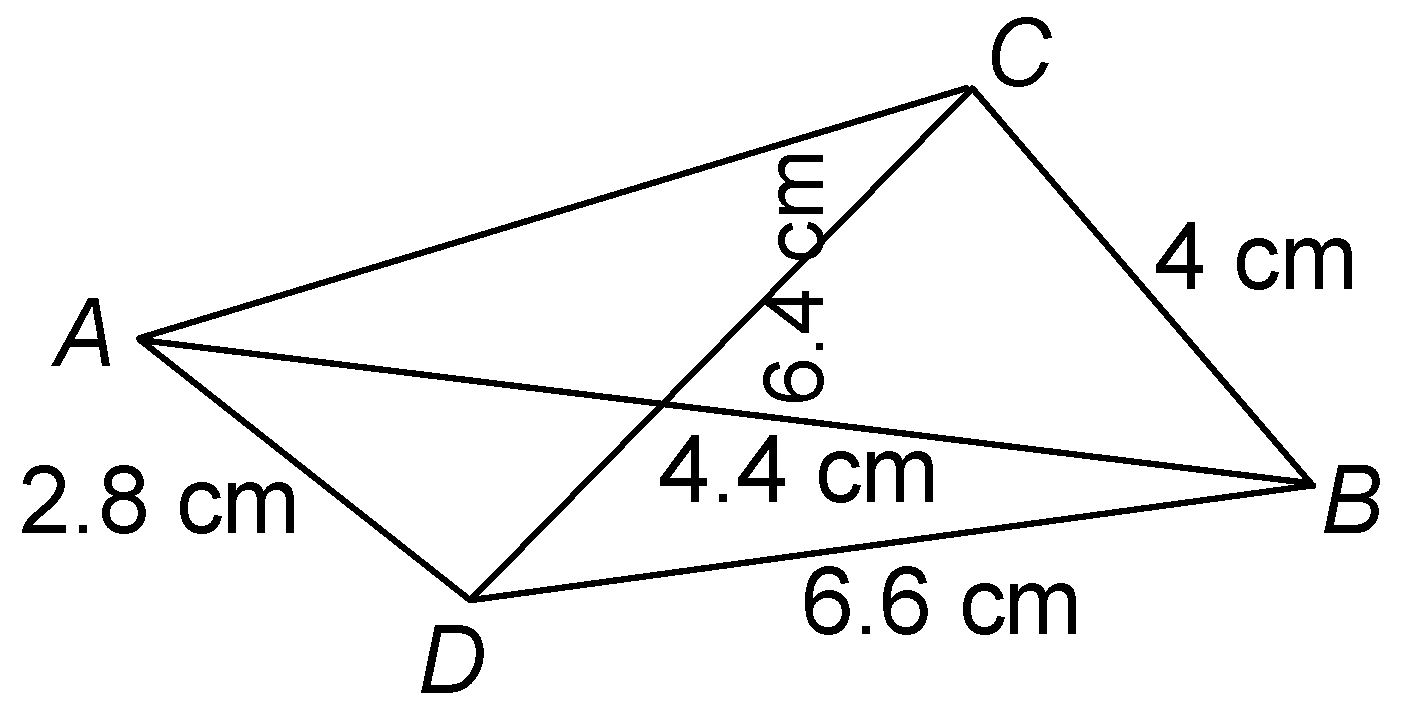
question 1. Construct a quadrilateral ADBC, in which AB = 4.4 cm, BC = 4 cm, CD = 6.4 cm, DA = 2.8 cm, and BD = 6.6 cm. Measure the length of AC.
|
Solution: Steps of construction
|
|
- With centre B and radius 4 cm, draw an arc. Then, with centre D and radius 6.4 cm, draw another arc which cuts the earlier arc of this step at the point C.
- Join BC and DC.
Thus, ABCD is the required quadrilateral.
Join AC. Length of AC = 6 cm.
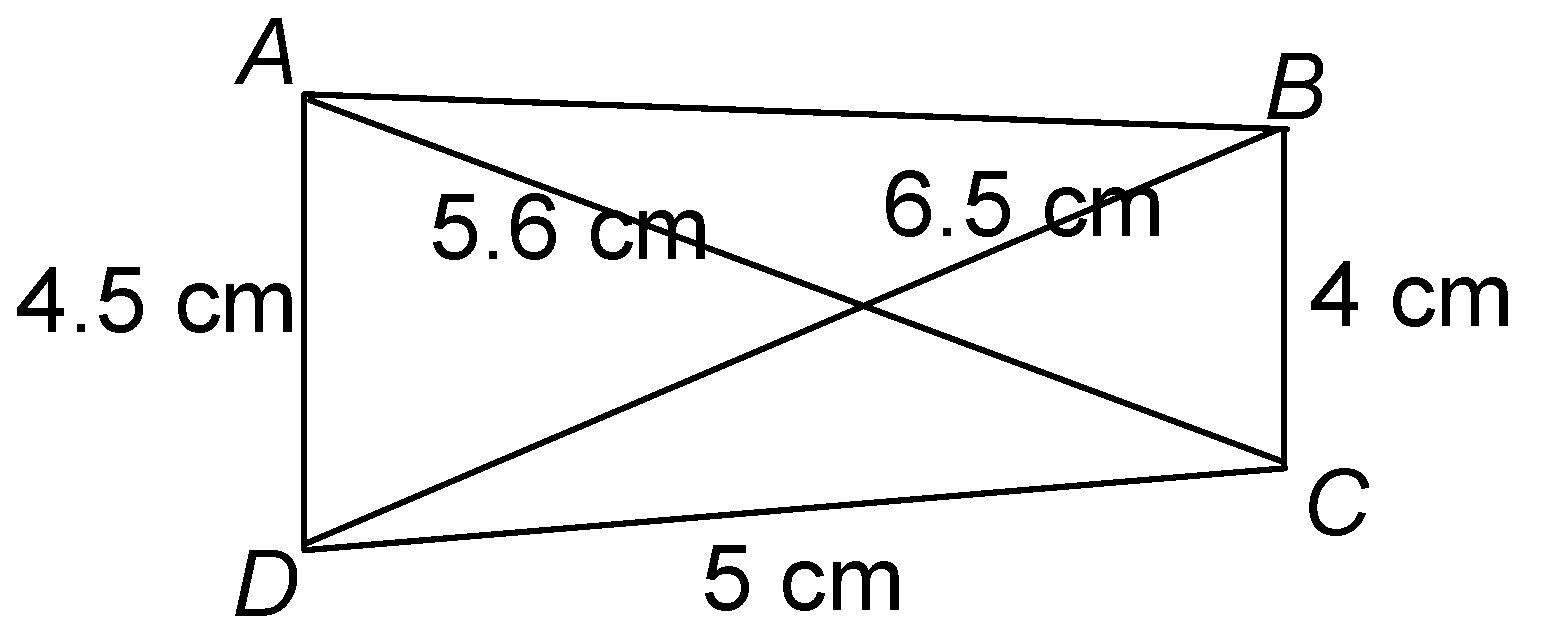
question 2. Construct a quadrilateral ABCD in which BC = 4 cm, CA = 5.6 cm, AD = 4.5 cm, CD = 5 cm, and BD = 6.5 cm.
|
Solution:Steps of construction
|
|
- Join DA and CA.
- With centre D and radius 6.5 cm, draw an arc. Then with centre C, and radius 4 cm, draw another arc which cuts the earlier arc of this step at point B.
- Join CB and B.
Thus, ABCD is the required quadrilateral.
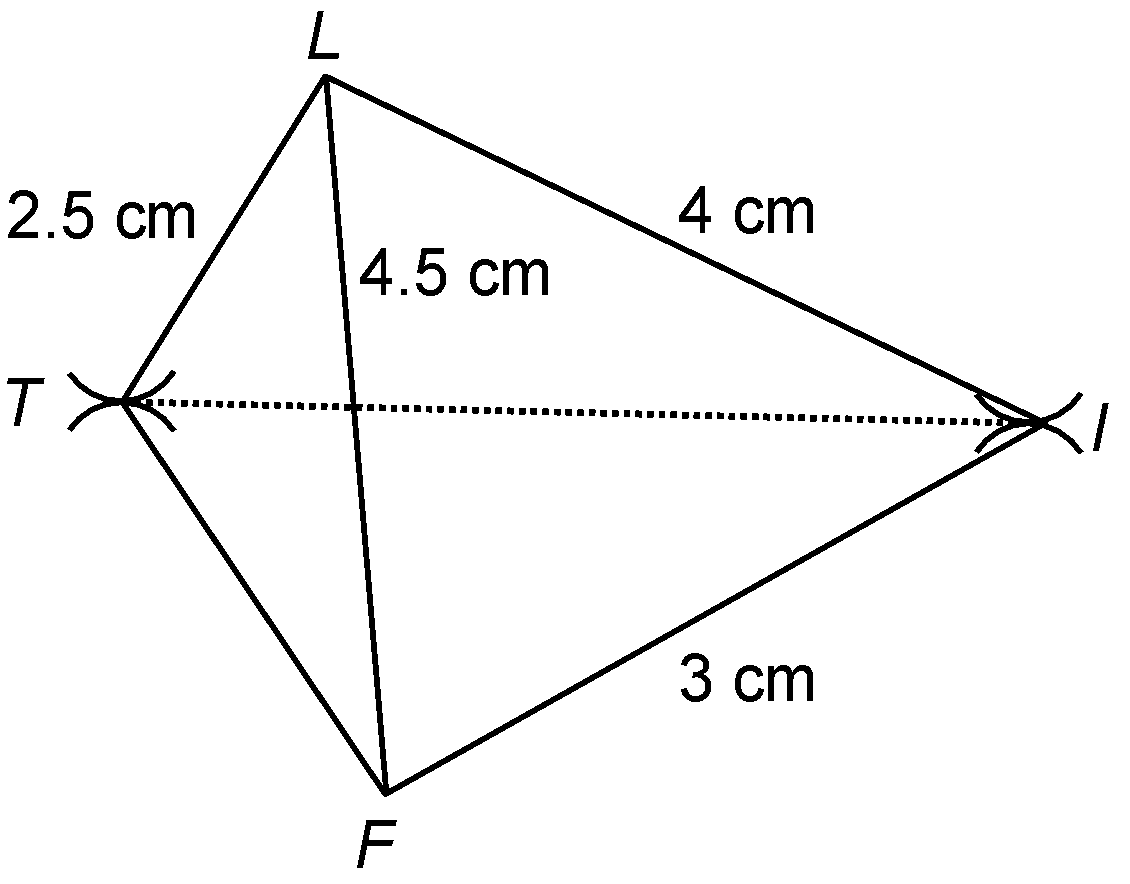
question 3. Construct the quadrilateral LIFT in which LI = 4 cm, IF = 3 cm, TL = 2.5 cm, LF = 4.5 cm and IT = 4 cm.
Solution:Steps of construction
- Take a line segment LF = 4.5 cm
|
|
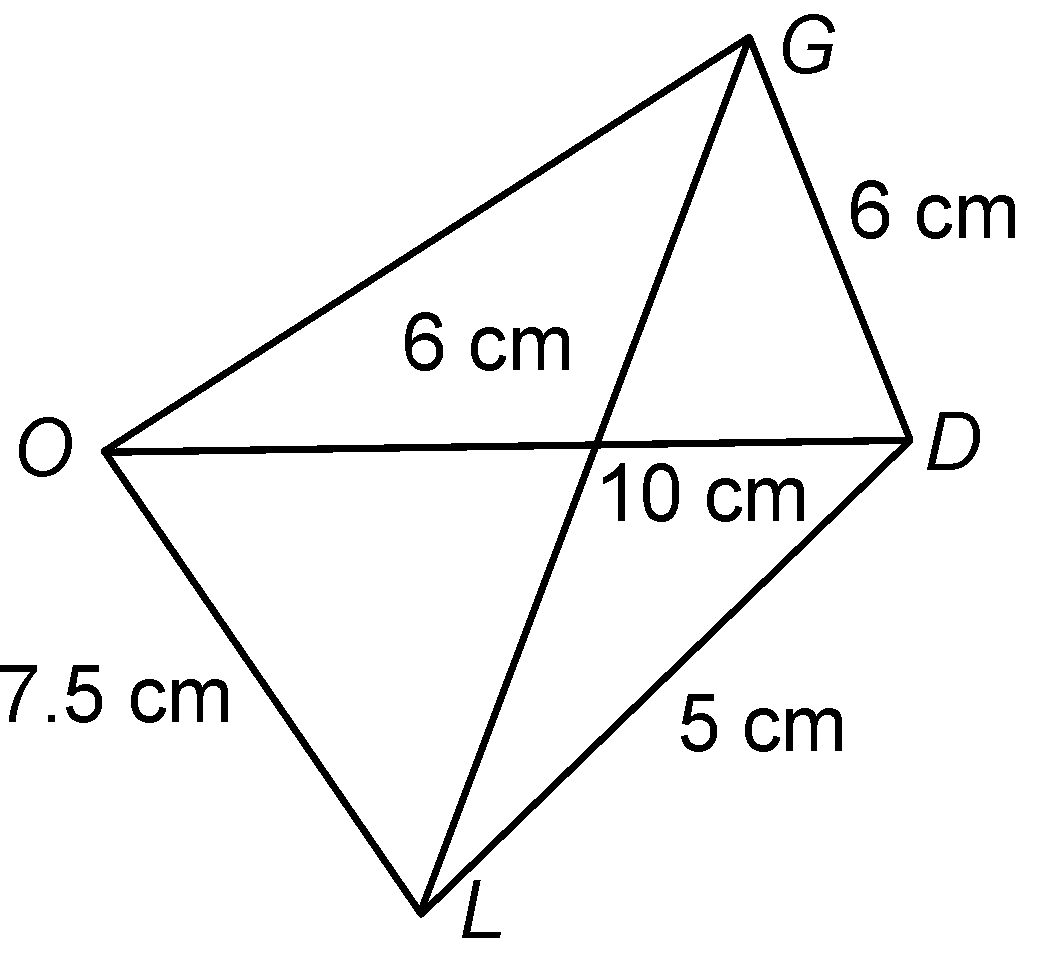
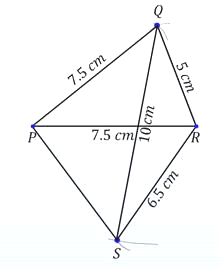
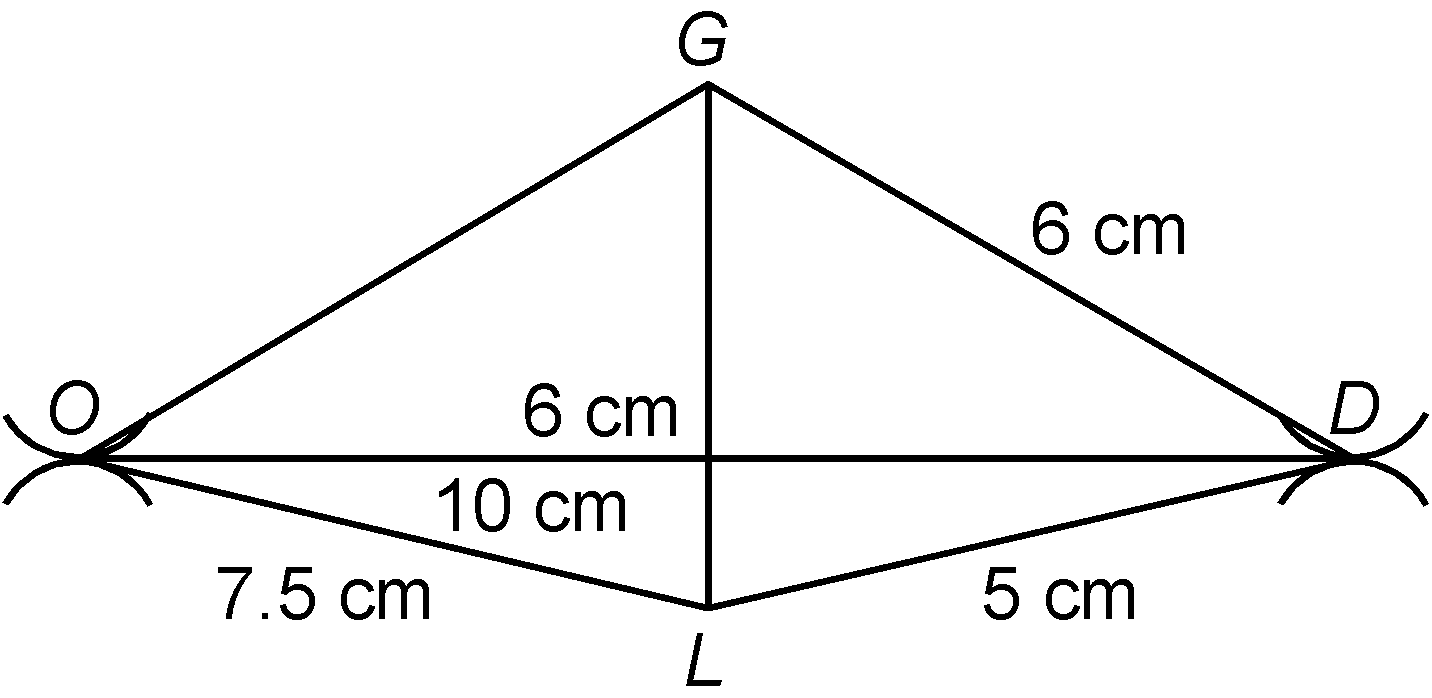
question 4. Construct the quadrilateral GOLD in which OL = 7.5 cm, GL = 6 cm, GD = 6 cm, LD = 5 cm and OD = 10 cm.
|
Solution: Here, GL = 6 cm GD = 6 cm and LD = 5 cm. Steps of construction
|
|
- Now, with L and D as centre cut off two arcs of length 7.5 cm and 10 cm respectively to obtain a point O.
- Join OL, OD and OG.
- Required quadrilateral GOLD is obtained.
CONSTRUCTING A QUADRILATERAL WHEN LENGTHS OF ITS ADJACENT SIDES AND THREE ANGLES ARE GIVEN:
Step 1: Draw a line segment of EF (say) of given length.
Step 2: Construct a given angle at E.
Step 3: Construct a given angle at F.
Step 4: Locate point G.
Step 5: Locate point H.
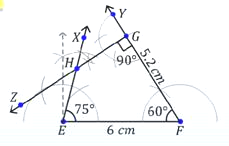
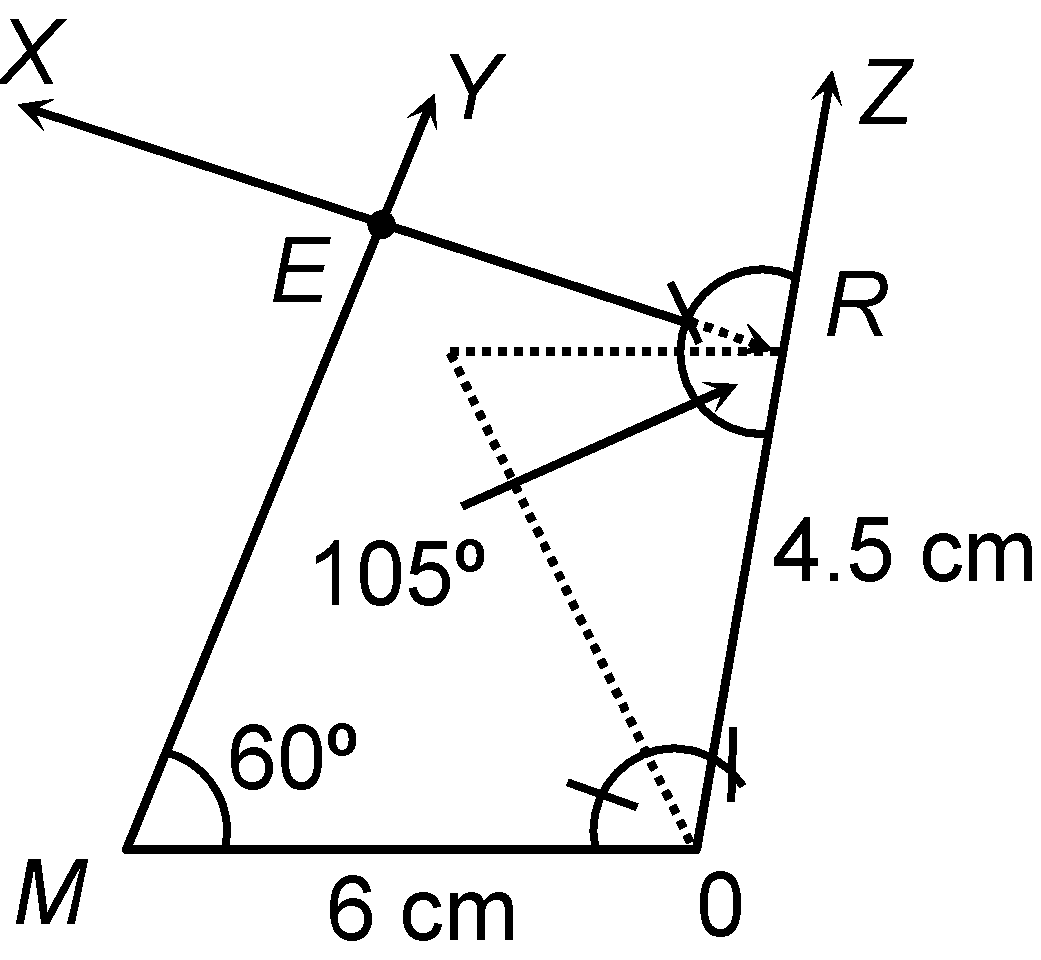
question 1. Construct the quadrilateral MORE in which MO = 6 cm, OR = 4.5 cm, ∠M = 60º, ∠O = 105º, ∠R = 105º.
Solution:
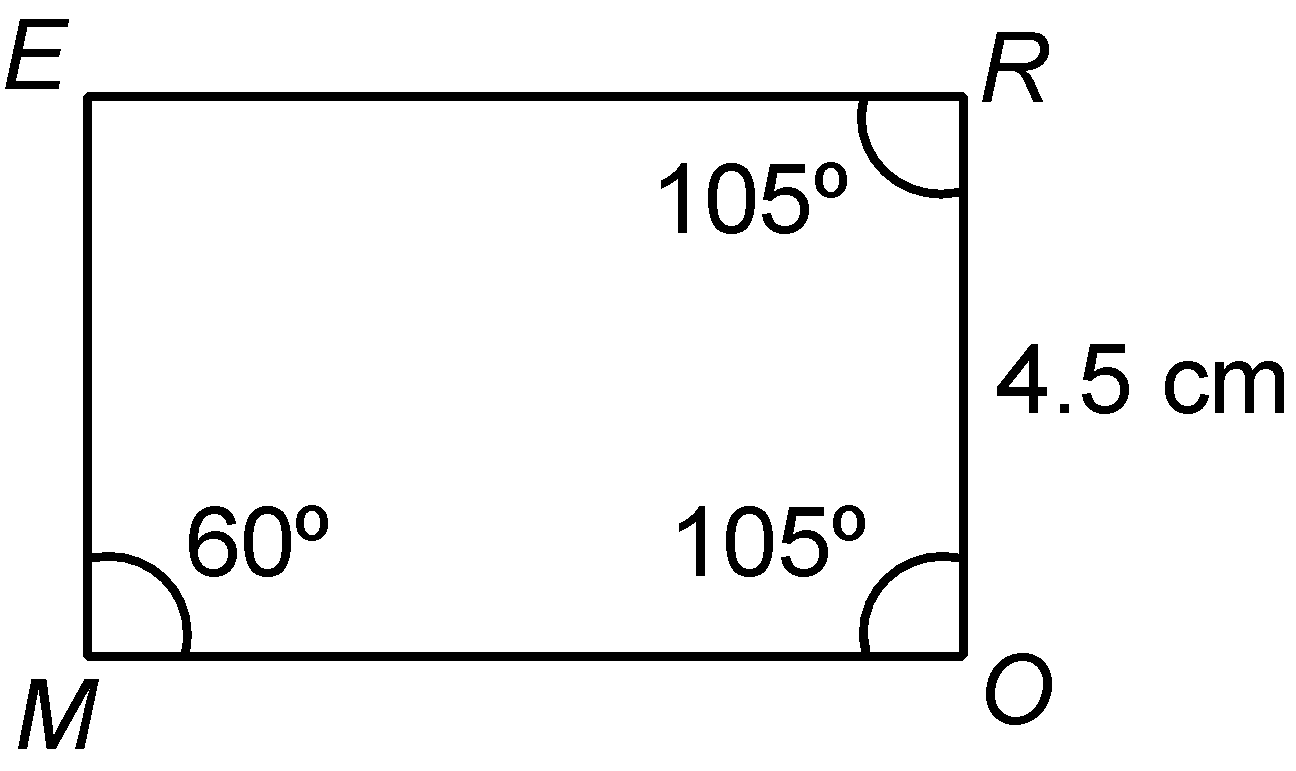
|
Steps of construction
|
|
question 2. Construct a rectangle OKAY in which OK = 7 cm and KA = 5 cm.
Solution:
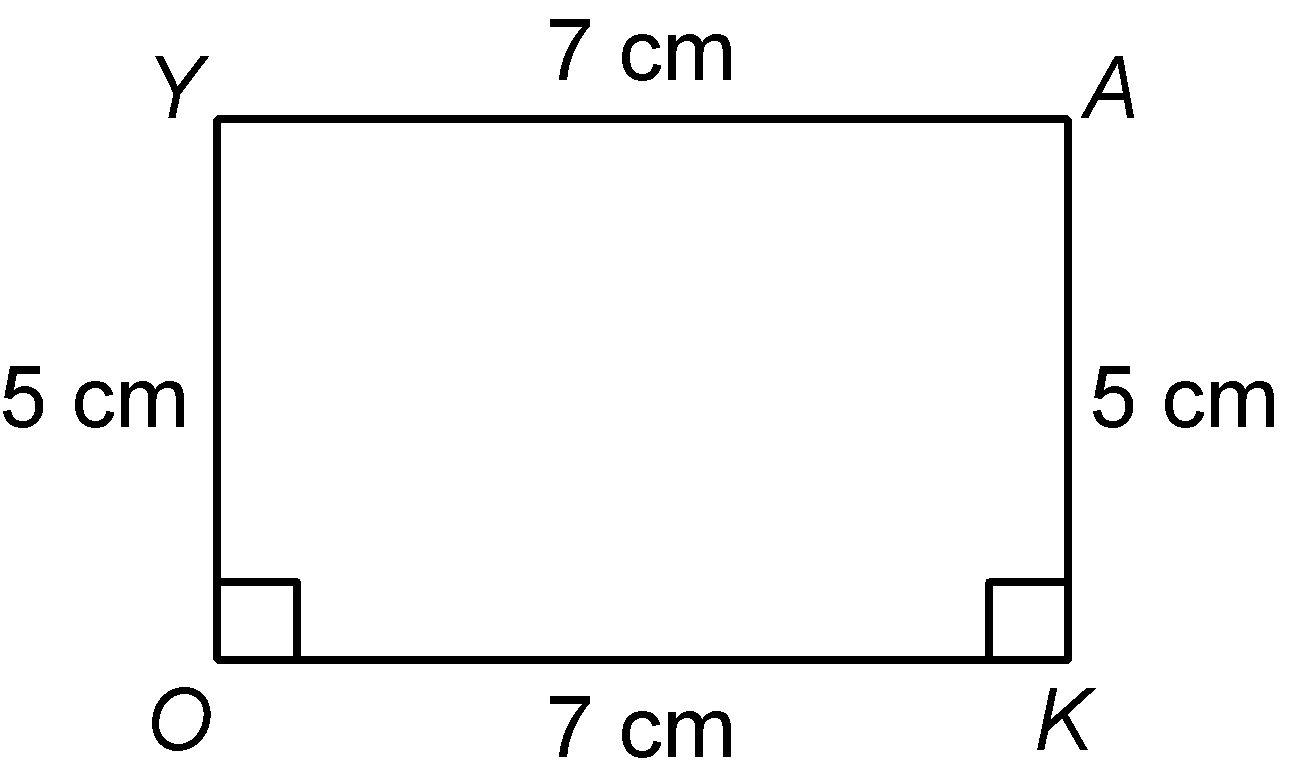
|
Steps of construction
|
|
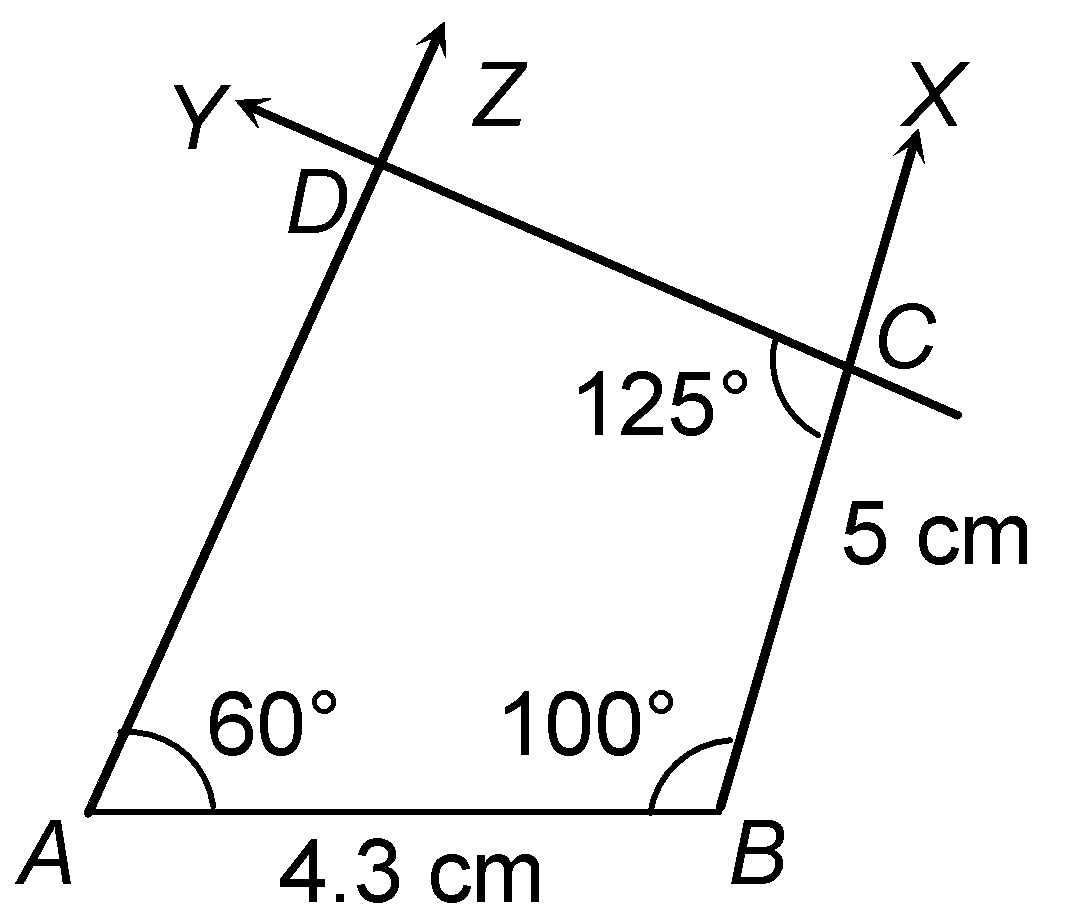
question 3. Construct a quadrilateral ABCD in which, AB = 4.3 cm, BC = 5 cm, ∠A = 60°, ∠B = 100° and ∠C = 125°.
|
Solution: Steps of construction
|
|
Then, ABCD is the required quadrilateral.
question 4. (i) Can a quadrilateral PLAN be constructed if PL = 6 cm, LA = 9.5 cm, ∠P = 75º, ∠L = 150º and ∠A = 140º.
(ii) In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct the parallelogram?
Solution: (i) ∠P + ∠L + ∠A = 365º
75º + 150º + 140º = 365º
Sum of four angles in a quadrilateral is 360º.
∴ Quadrilateral is not possible to construct.
(ii) No, it is not required to have the measure of angles because opposite sides of a parallelogram are equal.
If AB and BC are given
then, AB = DC, BC = AD.
CONSTRUCTING A QUADRILATERAL WHEN LENGTHS OF ITS THREE SIDES AND TWO DIAGONALS ARE GIVEN:
STEPS:
Step1: Draw a rough sketch of the quadrilateral PQRS.
|
Step 2: Draw a line segment of given length. Step 3: Construct the two given angles at two ends of the line. Step 4: With centre O and radius of the given length, draw an arc. Step 5: With centre R and radius of thje second side, draw another arc. Step 6: Join the two arcs |
|
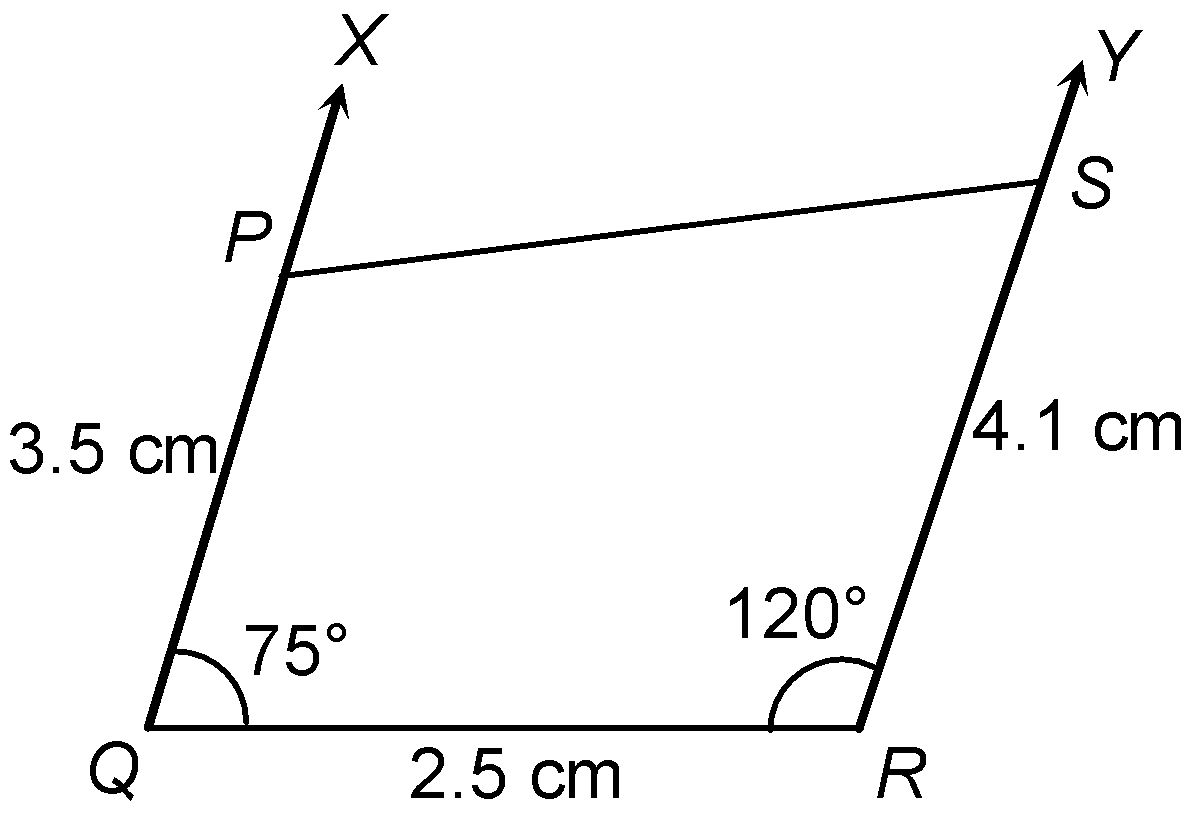
question 1. Construct a quadrilateral PQRS in which PQ = 3.5 cm, QR = 2.5 cm, RS = 4.1 cm, ∠Q = 75° and ∠R = 120°. Measure side PS.
Solution:Steps of construction
- Draw a rough sketch of the quadrilateral PQRS.
|
|
- Join PS.
Thus, PQRS is the required quadrilateral.
Measuring PS we find that PS = 3.7 cm.
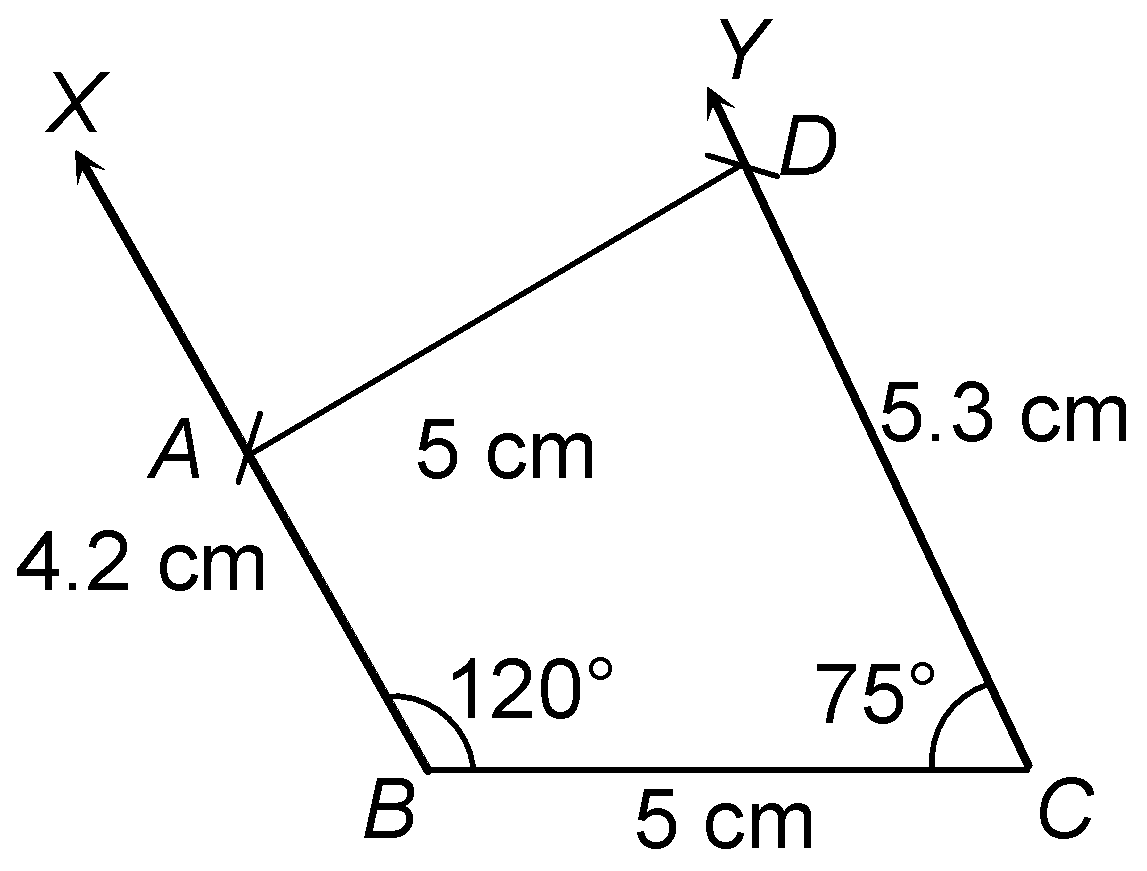
question 2. Construct a quadrilateral ABCD in which, AB = 4.2 cm, BC = 5 cm, CD = 5.3 cm, ∠B = 120° and ∠C = 75°.
|
Solution: Steps of construction
|
|
- Join DA.
Thus, ABCD is the required quadrilateral.
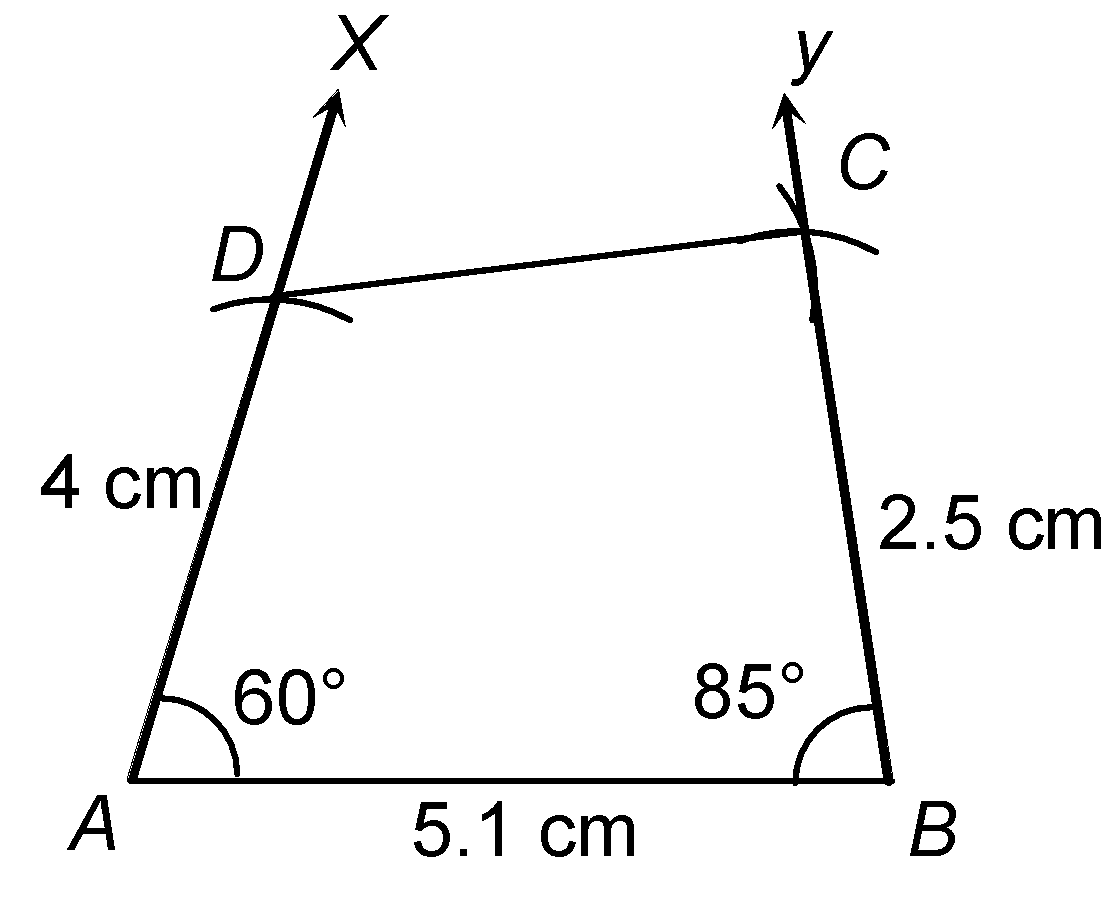
question 3. Construct a quadrilateral ABCD given AB = 5.1 cm, AD = 4 cm, BC = 2.5 cm, ∠A = 60° and ∠B = 85°.
Sol. Steps of construction
|
|
- Join CD.
The quadrilateral ABCD so obtained is the required quadrilateral.
question 4. (i) Can a quadrilateral ABCD be constructed with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and ∠B = 80º?
(ii) Can a quadrilateral PQRS be constructed with PQ = 4.5 cm, ∠P = 70º, ∠Q = 100º, ∠R = 80º and ∠S = 110º?
Solution:(i)
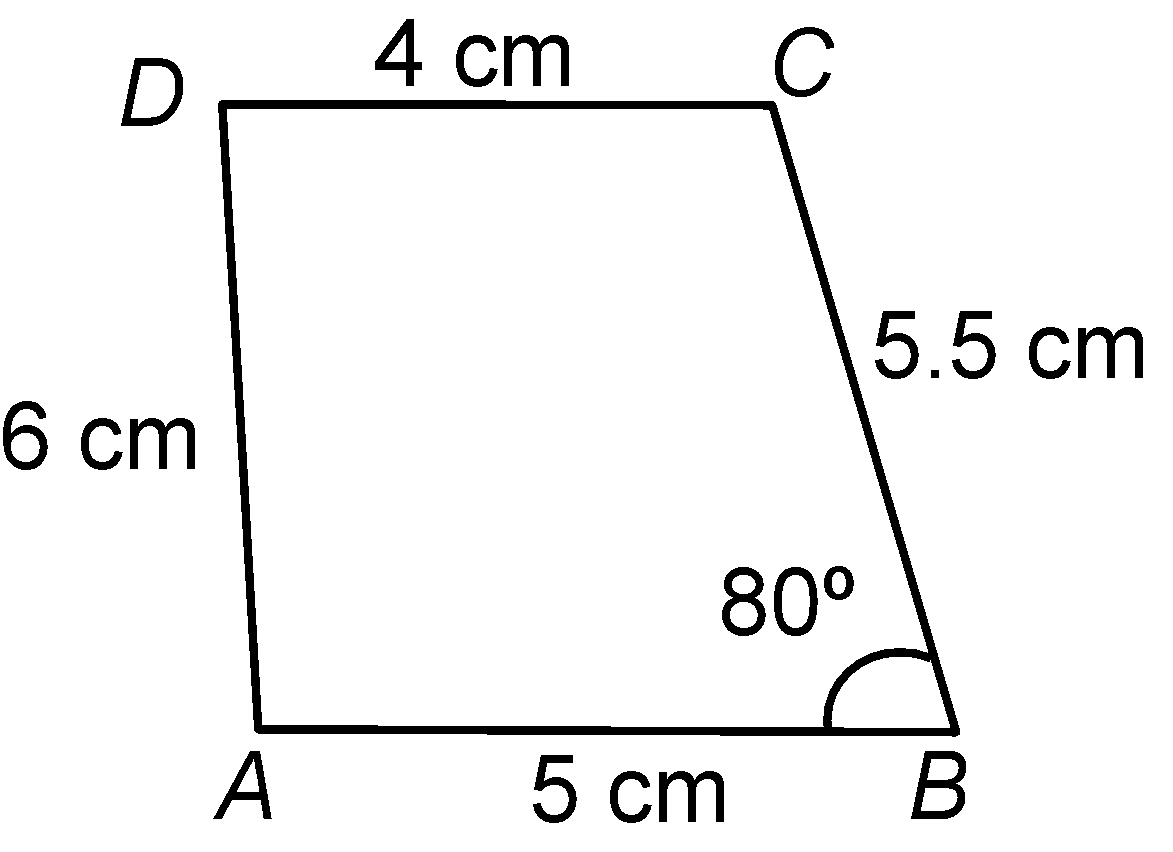
We can construct a quadrilateral ABCD with four sides and one angle.
(ii)
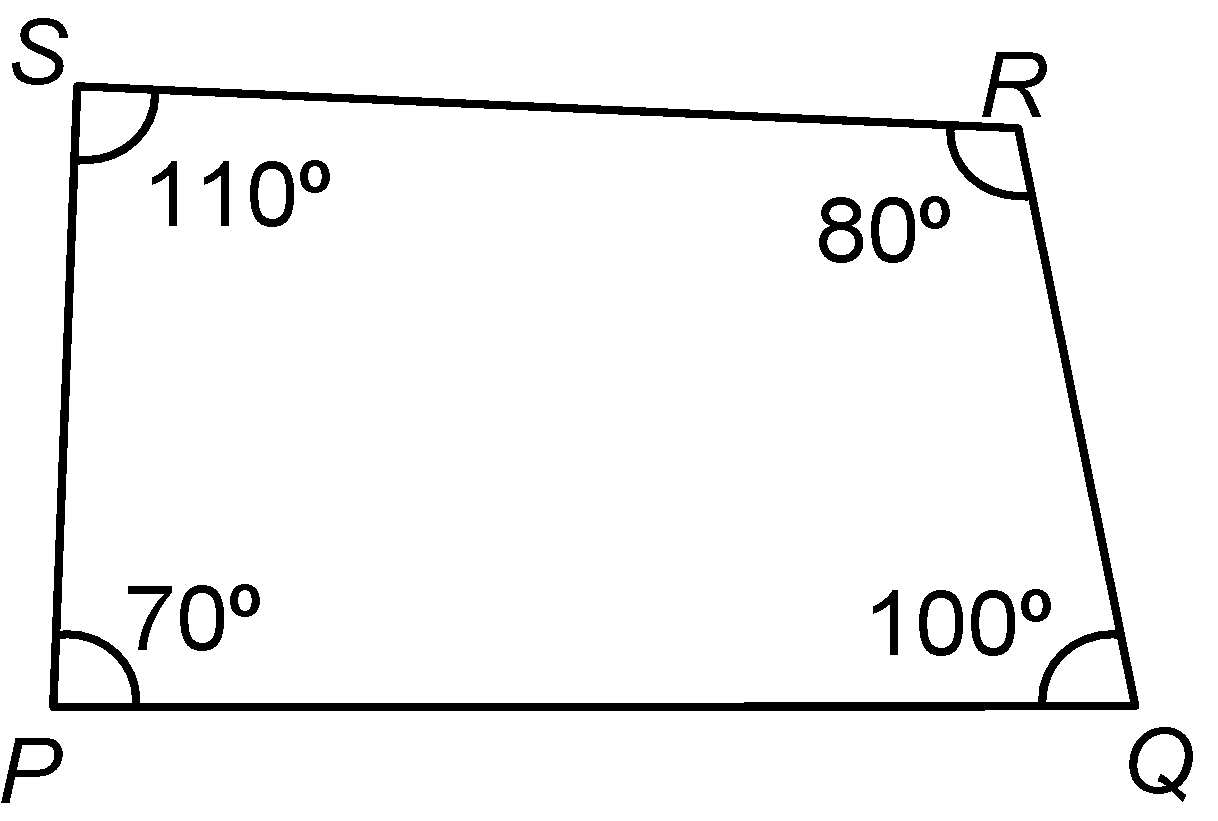
Here, at least one side RQ or PS is required. So, data is in-sufficient. Construction is possible only if
(a) two angles and two sides, e.g. if ∠A = 90º, ∠B = 90º, AD = 6 cm, BC = 5 cm. are given.
(b) four angles and two sides e.g. PQ = 4.5 cm, ∠P = 65º, ∠Q = 110º, ∠QR = 4.7 cm ∠R = 115º are given.
SPECIAL CASES QUADRILTERALS
A quadrilateral can be constructed using properties of specified quadrilateral.
PARALLELOGRAM
SQUARE
RECTANGLE |
|
- Opposite sides are equal.
- Diagonals are equal.
- Each angle 90º.
RHOMBUS
- Diagonals bisect each other at 90º.
- All sides are equal.
- Diagonals are unequal.
STEPS:
Step 1: Draw a side of given leng
Step 3: Draw side CE (say) of length th (say) CL
Step 2: Draw side LU (say) of given length perpendicular to CL at L. equal to LU and perpendicular to CL at C.
Step 4: Draw side UE.
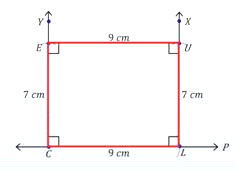
STEPS:
Step 1: Draw diagonal (say) AY and its perpendicular bisector.
Step 2: Draw sides say AL and AZ of given length.
Step 3: Draw sides LY and YZ.