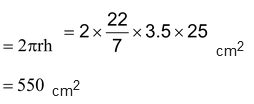VOLUME OF A CUBE AND A CUBOID

Volume of Cuboid 

The volume of a cuboid is the quantity that's used to measure the space in a cuboid. The cuboid is a 3D shape that can be seen around us very often. During this short lesson, we'll learn to find the volume of a cuboid. We will also learn to deduce the formula of volume of cuboid using a rectangular sheet and perceive a way to apply the formula also. As we already know both cube and cuboid are in 3D shape, whose axes go along the x-axis, y-axis and z-axis plane

Volume of cuboid = (length) × (breadth) × (height)

= l × b × h

So, V = lbh cubic unit …(i)

Volume of cube =  a × a × a cubic unit

So, 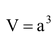cubic unit

Where  a = side of cube

From (i), it is clear that 

length

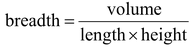
Question.  A matchbox measures 4 cm × 2.5 cm × 1.5 cm. What will be the volume of a packet containing 12 such boxes?

Solution: A matchbox is in the form of a cuboid.

∴ Volume of one match box = (4 × 2.5 × 1.5) cm3 = 15 cm3 [ Volume = ×b×h]

Hence, Volume of a packet containing 12 match boxes = 12 × 15 cm3 = 180 cm3

Ex. The volume of a cuboid is 440 cm3 and the area of its base is 88 cm2. Find its height.

Solution:  We have, 

Volume = 440 cm3 and area of the base = 88 cm2 

Height = 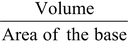⇒ Height =   440/88cm = 5 cm

CYLINDER:

Curved surface area of cylinder (C.S.A.) : It is the area of surface from which the cylinder is formed. When we cut this cylinder, we will find a rectangle with length 2πr are height h units.

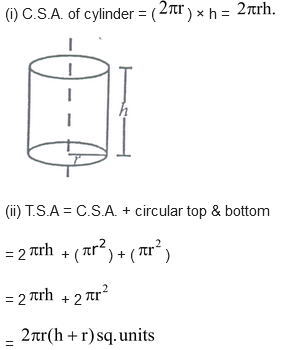
(iii) Volume of cylinder = Area of base × height

Hollow cylinder : 

(i) C.S.A. of hollow cylinder = (R + r)h sq. units

(ii) T.S.A. of hollow cylinder = (R + r)h + π(R₂ – r2)

= π(R + r) [2h + R - r] sq. units

(iii) Volume of hollow cylinder = π(R₂ – r₂)h cubic units

Where, r = inner radius of cylinder

R = outer radius of cylinder

h = height of the cylinder

Question.  Savitri had to make a model of a cylindrical kaleidoscope for her science project. She wanted to use chart paper to make the curved surface of the kaleidoscope. What would be the area of chart paper required by her, if she wanted to make a kaleidoscope of length 25 cm with a 3.5 cm radius? 

Solution: Radius of the base of the cylindrical kaleidoscope (r) = 3.5 cm.

Height (length) of kaleidoscope (h) = 25 cm.

Area of chart paper required = curved surface area of the kaleidoscope

Question. The curved surface area of a right circular cylinder of height 14 cm is 88 cm². Find the diameter of the base of the cylinder.

Solution:  Let r be the radius and h be the height of the cylinder. Then, 

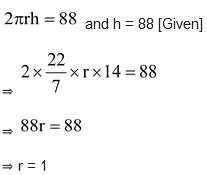
∴ Diameter of the base = 2r = 2 cm