SOME INEQUALITY RELATIONS IN A TRIANGLE

SOME INEQUALITY RELATIONS IN A TRIANGLE

If two sides of a triangle are unequal, the longer side has greater angle opposite to it.

Given:AΔ ABC in which AC>AB

To prove:∠ABC>∠ACB

Construction: Mark a point D on AC such that AB = AD. Join BD.

Proof : In ΔABD, we have

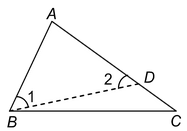
AB = AD [By construction]

⇒ ∠1 = ∠2 [ Angles opp. to equal sides are equal] …(i)

∠2 is the exterior angle of ΔBCD and an exterior angle is always greater than interior opposite angle. Therefore,

∠2 >∠DCB

⇒ ∠2 >∠ACB [∠ACB = ∠DCB] …(ii)

From (i) and (ii), we have

⇒ ∠1 >∠ACB …(iii)

∴ ∠ABC>∠1 …(iv)

From (iii) and (iv), we get

∠ABC>∠ACB

THEOREM:

In a triangle the greater angle has the longer side opposite to it.

Given : A Δ ABC in which ∠ABC>∠ACB

To prove :AC>AB

Proof : In ΔABC, we have the following three possibilities

(i) AC = AB

(ii) AC <AB

(iii) AC >AB

Case I : When AC = AB

If AC = AB

⇒ ∠ABC = ∠ACB [Angle opp. to equal sides are equal]

This is a contradiction, 

Since∠ABC>∠ACB [Given]

∴ AC≠AB

Case II : When AC<AB

if ∠AC<AB

⇒ ∠ACB>∠ABC [ Longer sides has the greater angle opposite to it]

This is also a contradiction

∴ We are left with the only possibility, AC>AB, which must be true

Hence, AC>AB

THEOREM:

The sum of any two sides of a triangle is greater than the third side.

Given: A Δ ABC

To prove:AB + AC>BC, AB + BC>AC and BC + AC>AB

Construction: Extend side BA to D such that AD = AC. Join CD

Proof: In ΔACD, we have

AC = AD [By construction]

⇒ ∠ADC = ∠ACD [Angles opp. to equal sides are equal]

⇒ ∠ACD = ∠ADC

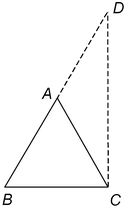
⇒ ∠BCA + ∠ ACD>∠ ADC [∠BCA + ∠ACD>∠ACD]

⇒ ∠BCD>∠ADC

⇒ ∠BCD>∠BDC [∠ADC = ∠BDC]

⇒ BD>BC [ Side opp. to greater angle is larger]

⇒ BA + AD>BC

⇒ BA + AC>BC [AC = AD (By construction)]

⇒ AB + AC>BC

Thus,AB + AC>BC

Similarly, AB + BC>AC and BC + AC>AB

Ex.10 In figure, PQ > PR, QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ > SR.

Solution: In ΔPQR, we have

PQ>PR [Given]

⇒ ∠PRQ>∠PQR [Angle opp. to larger side of a triangle is greater]

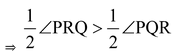
⇒ ∠SRQ>∠SQR

[RS and QS are bisectors of ∠PRQ and ∠PQR respectively]

⇒ SQ>SR [Side opp. to greater angle is larger]

Ex.11 In figure, sides LM and LN of ΔLMN are extended to P and Q respectively.
If x > y, show that LM > LN.

Sol. We have

∠LMN + x = 180° [Angles of a linear pair] …(i)

⇒ ∠LNM + y = 180° [Angles of a linear pair] …(ii)

∴ ∠LMN + x = ∠LNM + y

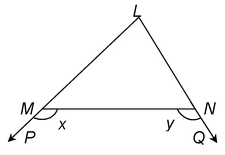
But, x>y [Given]

∴ ∠LNM>∠LMN

⇒ LM>LN

[Side opp. to greater angle is larger]