Types of triangles

TYPES OF TRIANGLES:

(i) On the basis of sides we have three types of triangles:

(A)Scalene triangle : A triangle whose no two sides are equal is called a scalene triangle.

(B) Isosceles triangle - A triangle having two sides equal is called an isosceles triangle.

(C) Equilateral triangle - A triangle in which all sides are equal is called an equilateral triangle.

(ii) On the basis of angles we have three types of triangles:

(A) Right triangle - A triangle in which any one angle is right angle (=90o) is called right triangle.

(B) Acute triangle - A triangle in which all angles are acute (>90o) is called an acute triangle.

(C) Obtuse triangle - A triangle in which any one angle is obtuse (<90o) is called an obtuse triangle.

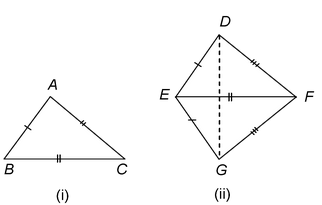
CONGRUENT FIGURES

The figures are called congruent if they have same shape and same size. In order words, two figures are called congruent if they are having equal length, width and height.

Fig. (i) Fig. (ii)

In the above figures {fig. (i) and fig. (ii)} both are equal in length, width and height, so these are congruent figures.

(a) Congruent Triangles :

Two triangles are congruent if and only if one of them can be made to superimposed on the other, so to cover it exactly.

If two triangles ΔABC and ΔDEF are congruent then there exist a one to one correspondence between their vertices and sides. i.e. we get following six equalities.

∠A = ∠D, ∠B = ∠E, ∠C = ∠F and AB = DE, BC = EF, AC = DF.

If two ΔABC &ΔDEF are congruent under A ⇔ D, B ⇔ E, C ⇔ F one to one correspondence then we write ΔABC≅ΔDEF we cannot write as ΔABC≅ΔDFE of ΔABC≅ΔEDF or in other forms because ΔABC≅ΔDFE have following one-one correspondence A ⇔ D, B ⇔ F, C ⇔ E.

Hence we can say that “two triangles are congruent if and only if there exists a one-one correspondence between their vertices such that the corresponding sides and the corresponding angles of the two triangles are equal.

(b) Sufficient Conditions for Congruence of two Triangles:

SAS Congruence Criterion:

Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other triangle.

Ex.1 In figure O is the mid-point of AB and CD. Prove that 

(i) ΔAOC ≅ΔBOD (ii) AC = BD and (iii) AC || BD

Sol: In Δs AOC and BOD, we have

AO = OB [O is the mid-point of AB]

∠AOC = ∠BOD [Vertically opposite angles]

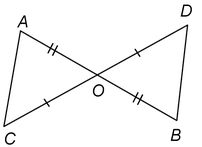
and, CO = OD [O is the mid-point of CD]

So, by SAS congruence criterion, we have

ΔAOC≅ΔBOD

⇒AC = BD and, ∠CAO = ∠DBO

[Corresponding parts of congruent triangles are equal]

Now, AC and BD are two lines intersected by a transversal AB such that 

∠CAO = ∠DBO, i.e. alternate angles are equal. Therefore, AC || BD

Ex.2 In figure, it is given that AE = AD and BD = CE. Prove that ΔAEB ≅ΔADC 

Solution: We have, 

∠EAB = ∠DAC [Common]

and, AC = AB [From (iii)]

So, by SAS criterion of congruence, we have

ΔAEB≅ΔADC

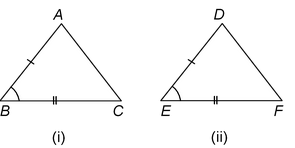
ANGLE-SIDE-ANGLE (ASA) CONGRUENCE CRITERION:

Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.

Given : Two Δs ABC and DEF such that ∠B = ∠E, ∠C = ∠F and BC = EF

To prove :ΔABC≅ΔDEF

Proof : There are three possibilities 

Case I : When AB = DE:

ΔABC≅ΔDEF

Case II : When BA<ED

In this case take a point G on ED such that EG = BA. Join GF.

ΔABC≅ΔGEF

⇒ ∠ACB = ∠GFE [cpct]

But, ∠ACB = ∠DFE [Given]

∴ ∠GFE = ∠DFE

This is possible only when ray FG coincides with ray FD or G coincides with D. 

Therefore, BA must be equal to ED.

Thus, in Δs ABC and DEF, we have

AB = DE [As proved above]

∠B = ∠E [Given]

and, BC = EF [Given]

So, by SAS criterion of congruence, we have

Hence, in all the three case, we have ΔABC≅ΔDEF

ANGLE- ANGLE-SIDE (AAS) CONGRUENCE CRITERION

If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.

⇒ ∠A + ∠B = ∠D + ∠E

⇒ 180°−∠C = 180°−∠F [Angle sum property]

⇒ ∠C = ∠F …(i)

Thus, in Δs ABC and DEF, we have

∠A= ∠D, ∠B = ∠E and ∠C = ∠F

Now, in ΔABC and ΔDEF, we have

∠B = ∠E [Given]

BC = EF [Given]

and,∠C = ∠F [From (i)]

So, by ASA criterion of congruence, ΔABC ≅ΔDEF

THEOREM:

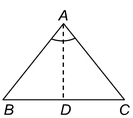
Angles opposite to equal sides of an isosceles triangle are equal.

Proof : In ΔBAD and ΔCAD

AB = AC [Given]

∠BAD = ∠CAD [By construction]

AD = AD [Common]

ΔBAD≅ΔCAD [By SAS Congruency]

∠ABD = ∠ACD [cpct]

∴∠B = ∠C

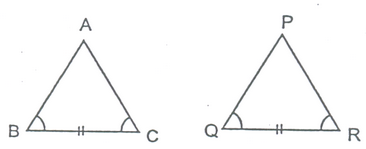
THEOREM:

If two angles of a triangle are equal, then sides opposite to them are also equal.

∠B = ∠C [Given]

∠BAD = ∠CAD [By construction]

AD = AD [Common]

So, by SAS criterion of congruence, we have

ΔABD≅ΔACD

⇒ AB = AC [cpct]

Ex.3 In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

Solution: Since diagonal AC bisects the angles A and C.

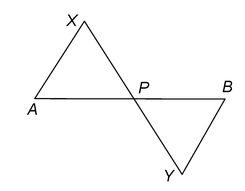
Ex.4 AB is a line segment, AX and BY are two equal segment drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P, prove that 

(i) ΔAPX ≅ΔBPY (ii) AB and XY bisect each other

Solution: Since AX || BY and transversal AB intersects them at A and B respectively. Therefore,

∠BAX = ∠ABY [Alternate angles] 

Similarly, we have ∠AXP = ∠BYP [Alternate angles]

⇒ AP = BP and PX = PY [cpct]

Hence, AB and XY bisect each other at P.

SIDE-SIDE-SIDE(SSS) CONGRUENCE CRITERION

Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.

BC = EF [Given]

AB = GE [By construction]

and, ∠ABC = ∠FEG [By construction]

So, by SAS criterion of congruence, we have

ΔABC≅ΔGEF

⇒ ∠A = ∠Gand AC = GF [c.p.c.t.]

Now, AB = DE and AB = GE …(i)

⇒ DE = GE

Similarly, AC = DF and AC = GF …(ii)

⇒ DF = GF

In ΔEGD, we have

DE = GE [From (i)]

⇒ ∠EDG = ∠EGD …(iii) [Angles opp. to equal side]

In ΔFGD, we have

DF = GF [From (ii)]

⇒ ∠FDG = ∠FGD …(iv) [Angles opp. to equal side]

From (iii) and (iv), we have

∠EDG + ∠FDG = ∠EGD + ∠FGD

⇒ ∠D = ∠G

But, ∠G = ∠A [Proved above]

∴ ∠A = ∠D …(v)

Thus, in Δs ABC and DEF, we have

AB = DE [Given]

∠A = ∠D [From (v)]

and, AC = DF [Given]

So, by SAS criterion of congruence, we have

ΔABC≅ΔDEF

RIGHT ANGLE-HYPOTENUSE-SIDE (RHS) CONGRUENCE CRITERION

Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle.

Given : Two right angles ABC and DEF in which ∠B = ∠E = 90°, AC = DF, BC = EF

To prove :ΔABC≅ΔDEF

Construction : Produce DE to G so that EG = AB. Join GF

Proof :In Δs ABC and ΔGEF, we have AB = GE [By construction] ∠ABC = ∠FEG [Both 90º] and,BC = EF [Given] So, by SAS criterion of congruence, we have ΔABC≅ΔGEF

⇒ ∠A = ∠G …(i)

AC = GF [cpct] …(ii)

Now, AC = GF [From (ii)]

and, AC = DF [Given]

∴ DF = GF

⇒ ∠D = ∠G [Angles opposite to equal sides] ...(iii)

From (i) and (iii), we get

∠A = ∠D …(iv)

Thus, in Δs ABC and DEF, we have

∠A = ∠D [From (iv)]

∠B = ∠E [Both 90º]

⇒ ∠A + ∠B = ∠D + ∠E

⇒ 180°−∠C = 180°−F [Angle sum property]

⇒ ∠C = ∠F …(v)

Now, in Δs ABC and DEF, we have

BC = EF [Given]

∠C = ∠F [From (v)]

and, AC = DF

So, by SAS criterion of congruence, we have

ΔABC≅ΔDEF

Ex.5 ABCD is a parallelogram, if the two diagonals are equal, find the measure of ∠ABC.

Solution: Since ABCD is a parallelogram. Therefore,

AB = CD and AD = BC [Opp. sides of a parallelogram are equal]

⇒ ∠BAD = ∠ABC [cpct] …(i)

Now, AD || BC and transversal AB intersects them at A and B respectively.

∴ ∠BAD + ∠ABC = 180° [Cons. Interior angles are supplementary]

⇒ ∠ABC + ∠ABC = 180° [From (i)]

⇒ 2∠ABC = 180°

⇒ ∠ABC = 90°

Hence, the measure of ∠ABC is 90°.

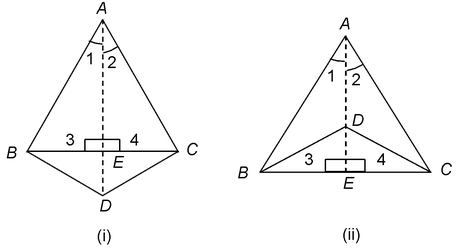
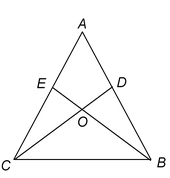
Ex.6 If two isosceles triangles have a common base, prove that the line joining their vertices bisects them at right angles.

Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.

To Prove:AD bisects BC at right angle.

Proof: In Δs ABD and ACD, we have

AB = AC [Given]

BD = CD [Given]

and,AD = AD [Common]

So, by SSS criterion of congruence, we have

ΔABD≅ΔACD

⇒∠1 = ∠2 …(i) [cpct]

∴ In ΔABE and ΔACE, we have

AB = AC [Given]

∠1 = ∠2 [From (i)]

and,AE = AE [Common]

So, by SAS criterion of congruence, we have

ΔABE≅ΔACE

⇒ BE = CE [cpct]

and, ∠3 = ∠4 [cpct]

But, ∠3 + ∠4 = 180° [Linear pair]

⇒ 2∠3 = 180° [∠3 = ∠4]

⇒ ∠3 = 90°

∴ ∠3 = ∠4 = 90°

Hence, AD bisects BC at right angles.

Ex.7 ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that 

(i)

(ii) AB = AC; i.e. ABC is an isosceles triangle.

Given:

In ΔABC altitudes BE = CF

To prove:(i)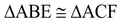

(ii) AB = AC ; i.e. ABC is an isosceles triangle.

Solution:

(i)In ΔABE and Δ ACF, we have

BE = CF[Given]

∠AEB = ∠AFC = 90o [ BE and CF are altitudes: Given]

and ∠A = ∠A[Common]

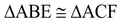[By AAS congruence rule] Proved. (ii)

[By proof]

∴ AB = AC[By CPCT]

Hence, ABC is an isosceles triangle.

Ex.8 ABC is a right angled triangle in which ∠A = 90o and AB = AC. Find ∠B and ∠C.

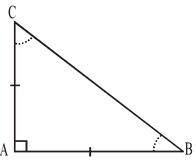
Given:

ABC is a right angled triangle in which ∠A = 90o and AB = AC.

To find:

∠B and ∠C

Solution:

In right angled triangle ABC, we have

AB = AC[Given]

∴∠B = ∠C

[Angles opposite to equal sides of a triangle are equal] ....(i)

Now, ∠A + ∠B + ∠C = 180o[Angles sum property of a Δ]

⇒ 90o + ∠B + ∠B = 180o[From (i) 

∠B = ∠C]

=> 2∠B = 180o – 90o⇒ 2∠B = 90o

=>∠B =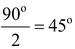

Hence, ∠B = ∠C = 45o

Ex.9 BE and CF are two equal altitudes of a triangle ABC. Prove that the triangle ABC is isosceles.

Given:

BE and CF are two equal altitudes of a triangle ABC, i.e., BE = CF 

and ∠AEB = ∠AFC = 90o

To prove:

ΔABC is isosceles.

Solution:

In ΔABE and ΔACF, we have

BE = CF[Given]

∠AEB = ∠AFC = 90o[Given]

and ∠A = ∠A[Common]

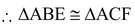
[By AAS congruence rule]

 AB = AC[By CPCT]

Hence, ΔABC is isosceles.Proved.