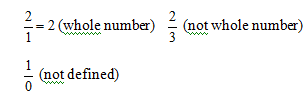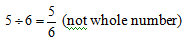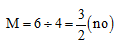Properties of Whole Numbers

Properties of whole numbers

Addition of two whole numbers: It will always lead to a whole number only.

0 + 1 = 1, 0 + 0 = 0, 1 + 2 = 3

Subtraction of whole number: It may or may not give result as a whole number

            0 – 1 = –1  (not whole number)

            1 – 2 = –1  ( not whole number)

            2 – 1 = 1  (whole number)

Multiplication of whole number: It will always give result as a whole number.

            0 × 1 = 0, 1 × 2 = 2, 2 × 3 = 6

Division of whole number: It may or may not give result as a whole number

Closure property: Whole numbers are closed under addition and multiplication but not under subtraction and division.

i.e.,      5 + 6 = 11 (whole number)

            5 × 6 = 30 (whole number

            5 – 6 = –1 (not whole number)

Illustration 3:

N = 6 – 4, M = 6 + 4, P = 2 × 1 , O = 4 – 6. Find out whether these numbers are whole numbers or not.

Sol.      N = 6 – 4 (yes)

            O = 4 – 6 = –2 (no)

            P = 2 × 1 = 2 (yes)

Commutativity: Whole numbers are commutative under addition and multiplication but not under subtraction and division.

            5 + 6 = 11 = 6 + 5

            5 × 6 = 30 = 6 × 5

            5 – 6 = –1 ¹ 6 – 5 = 1

            5 ÷ 0 ¹ 0 ÷ 5

            5 ÷ 6 ¹ 6 ÷ 5

Associativity: In repeated multiplication/addition, the order of doing calculation does not make any impact on final answer. But this is not true for division / subtraction. If a, b, c is whole numbers then

a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.

Illustration 4:

Is 2 + (3 + 4) = (2 + 3) + 4

Sol.      L.H.S. = 2 + (3 + 4) = 2 + 7 = 9

            R.H.S = (2 + 3) + 4 = 5 + 4 = 9

            L.H.S. = R.H.S.

            \ Answer is yes.

Illustration 5:

Is 2 × (3 × 4) = (2 × 3) × 4

Sol.      2 × 12 = 6 × 4

            L.H.S. 2 × (3 × 4)

            = 2 × 12 = 24

            R.H.S. (2 × 3) × 4 = 6 × 4 = 24

             L.H.S. = R.H.S.

            \Answer is yes.

Distributivity of multiplication over addition/subtraction

If a, b and c are whole numbers then

a × (b + c) = a × b + a × c

a × (b – c) = a × b – a × c

            2 × (3 + 4) = 2 × 3 + 2 × 4

            5 × (10 + 1) = 5 × 10 + 5 × 1

            5 × (100 – 1) = 5 × 100 – 5 × 1

This property can be used to make calculation easier.

Illustration 6:

Solve 15 × 99 using distributive property

Sol.      15 × (100 – 1)

            = 15 × 100 – 15 × 1 = 1500 – 15 = 1485.

Additive and multiplicative identity

1 + 0 = 1, 2 + 0 = 2, 3 + 0 = 3, 4 + 0 = 4 so on.

1 × 1 = 1, 2 × 1 = 2, 3 × 1 = 3, 4 × 1 = 4 so on.

If we add ‘0’ to any number result will always be the same number.

If we multiply ‘1’ to any number, result will always be the same number.

Therefore, ‘0’ is the additive identity for whole number and 1 is the multiplicative identity for whole number.