Direction cosines and direction ratios

Direction cosines and direction ratios

Direction Cosines

If α, β, γ are the angles which a vector makes with the positive directions of the coordinates axes OX, OY, OZ respectively, then cosα, cosβ, cosγ are known as the direction cosines of and are generally denoted by the letters l, m, n respectively i.e. l = cosα, m = cosβ, n = cosγ.

The angles α, β, γ are known as the direction angles and satisfy the condition 0 ≤ α,β, γ ≤ π.

Some Results on Direction Cosines

Let P(x, y, z) be a point in space such that has direction cosines l, m, n. Then

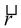(i) are projections of on OX, OY, OZ respectively.

(ii) x = l |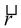|, y = m |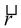|, z = n||

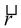(iii) 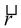 = ||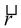 (l + m + n) and = l + m+ n

(iv)  l₂ + m₂ + n₂ = 1

Direction Ratios

If l, m, n are direction cosines of a vector, then l₂ + m₂ + n₂ = 1. Therefore, l, m, n usually involve fractions and radical signs.

Let l, m, n be direction cosines of a vector 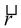and a, b, c be three numbers such that

Then a, b, c are known as direction ratios or direction number of vector 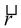.