De Moivers Theorem
Complex Numbers of Class 11
De Moiver's Theorem
- If n is a +ve integer then (cosθ + i sinθ)n = cosnθ + i sinnθ
- If n is rational then one of the values of (cosθ + i sinθ)n is (cos nθ + i sinnθ)
- nth roots of a complex number
If z = r(cosθ + i sinθ) = r{cos(2mπ + θ) + i sin(2mπ + θ)}
Hence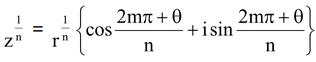 
where m = 0, 1, 2, 3 …. (m − 1)
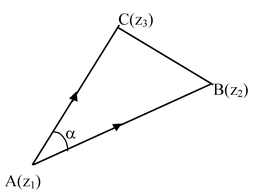
If z1 z2 z3 be the affixes of the vertices of the triangle ABC described in the anticlock wise sense then
= 
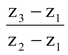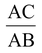(cosα + i sinα)
where ∠BAC = α
The lines joining the points z1, z2 and z3, z4 will be perpendicular if and only if
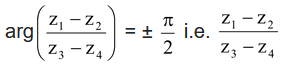is purely imaginary.
