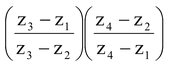General Equation Of A Circle
Complex Numbers of Class 11
General Equation of A Circle
Let us consider a circle with center at C(z0) with radius r and P any point on the circle.
Then PC = r = |z −z0|
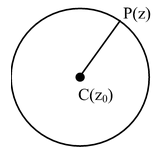
⇒ |z − z0|2 = r2 ⇒ (z − z0)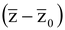 = r2
= r2
⇒ 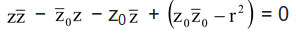
⇒ 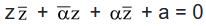 where a =
where a = 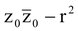 is real and α = − z0
is real and α = − z0
The center of the circle is −α and radius = 
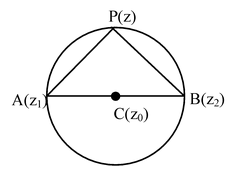
Circle described on the line segment joining z1 and z2 as diameter is
|
(z − z1)
Clearly ∠APB =
∴ arg
∴ |
|
|
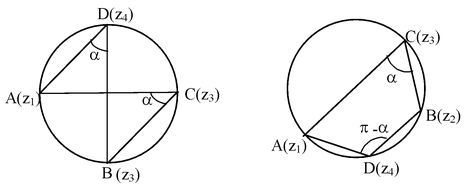
Condition for the four points z1, z2, z3 and z4 to be concyclic is
is real Let the points A(z1) B(z2) C(z3) and D(z4) be concylic |
|
Then ∠ACB and ∠ADB are either equal or different by π
So arg 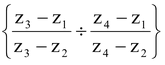 is either O or π.
is either O or π.
i.e.  is real
is real
 + (z − z2)
+ (z − z2) 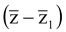 = 0
= 0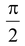
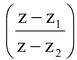 =
= 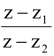 is purely imaginary.
is purely imaginary.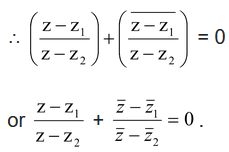 .
.