Conversion Of Solid From One Shape To Another

Conversion Of Solid From One Shape To Another

For commercial works and for industrial development work, we need to convert a solid into another solid of different shape or more than one solid of similar shape but with reduced size.

The calculation of surface areas and volumes in above cases will be illustrated below.

question 1. A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?

Solution: Let r be the radius of a cylinder, a cone and a hemisphere respectively and h be the height of the cylinder, a cone and a hemisphere respectively.

Then, h = r

V₁ =  Volume of a cylinder = πr²h, V₂ = Volume of a cone = 1/3πr²h

and V_{3 =} Volume of a hemisphere = 2/3πr²

∴

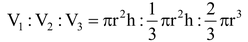
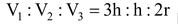⇒ [∴ r = h in case of hemisphere]

⇒

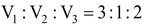
question 2. A solid sphere of radius r is the melted and cast into the shape of a solid cone of height r, find the radius of the base of the cone.

Solution: Volume of a solid sphere of radius r = Volume of cone of base r₁ and height r

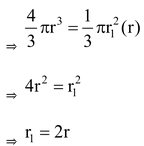
Thus, the radius of the base of the cone is 2r.

question 3. A metallic sphere of radius 10.5 cm is melted and then recast into smaller cones, each of radius 3.5 cm and height 3 cm. How many cones are obtained?

Solution: Radius of the sphere = 21/2 cm.

Volume of the sphere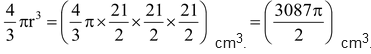

Radius of each cone = 7/2 cm and its height = 3 cm.

Volume of each cone .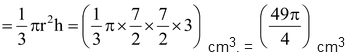

Required number of cones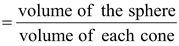

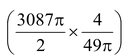= = 126.

question 4. The internal and external radii of a hollow sphere are 3 cm and 5 cm respectively. The sphere is melted to form a solid cylinder of height 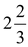cm. Find the diameter and the curved surface area of the cylinder.

Solution: External radius of the sphere = 5 cm.

Internal radius of the sphere = 3 cm.

Volume of metal in the hollow sphere .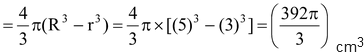

Let the radius of the solid cylinder be r cm.

Height of the solid cylinder = 8/3 cm.

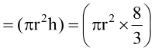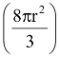Volume of the solid cylinder cm³= cm³.

Volume of cylinder = Volume of metal in hollow sphere.

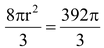∴ ⇒ r² = 49 ⇒ r = 7.

Hence, the diameter of the cylinder formed= (2 x 7) cm = 14 cm.

Curved surface area of the cylinder

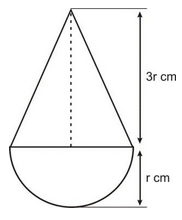
question 5. A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere and total height of the toy, if the height of the cone is 3 times the radius.

Solution: Radius of the cylinder = 6 cm.

Height of the cylinder = 15 cm.

Volume of the cylinder = (πr²h) = (π x 6 x 6 x 15)

 = (540π) cm³.

Volume of 12 toys = (540π) cm3.

Volume of 1 toy =(540π/12)= (540π/12) cm³= (45π) cm³.

Let the radius of the hemisphere be r cm.

Then, the height of the cone = 3r cm.

Volume of 1 toy = volume of hemisphere + volume of cone

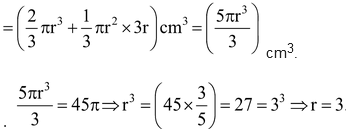
Radius of the hemisphere = 3 cm.

Total height of the toy = (r + 3r) cm = (4r) cm

= (4× 3) cm = 12 cm.

question 6. A well, whose diameter is 7m, has been dug 22.5 m deep and the earth dugout is used to form an embankment around it. If the height of the embankment is 1.5m, find the width of the embankment.

Solution: Radius of the well  = 7/2 m = 3.5m.

Depth of the well = 22.5 m.

∴ Volume of the earth dugout  = π x (3.5)² x 22.5 m³

m³

Let the width of the embankment be r metres.

Embankment forms a cylindrical shell whose inner and outer radii are 3.5 m and (r + 3.5) m respectively and height 1.5 m.

∴ Volume of the embankment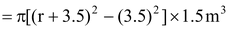

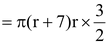m³.

But,Volume of the embankment = Volume of the earth dugout

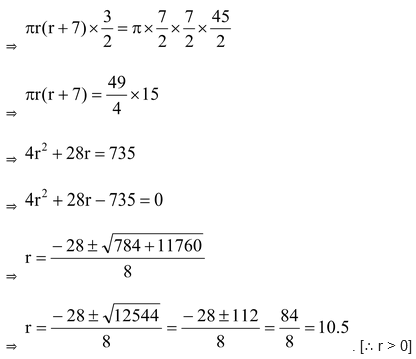
Hence, the width of the embankment is 10.5 m.