Frustum Of A Cone

When a cone is cut by a plane parallel to base, a small cone is obtained at top and other part is obtained at bottom. This is known as ‘Frustum of Cone’.

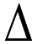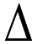ABC ~ ADE

Volume of Frustum:

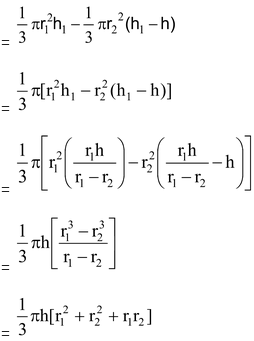
Curved Surface Area of Frustum:

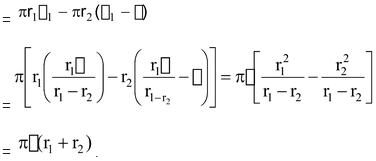
Total Surface Area of Frustum:

= CSA of frustum +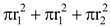

=

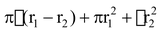
Slant height of a Frustum:

=

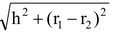
where,

h - height of the frustum

r₁ = radius of larger circular end

r₂ = radius of smaller circular end

Question 1. The decorative block is made of two solids – a cube and a hemisphere. The base of the block is a cube with edge 5 cm and the hemisphere fixed on the top has a diameter of 4.2 cm, find the total surface area of the block. (Take π = 22/7)

Solution: The total surface area of the cube = 6 × (edge)² = 6 × 5 × 5 cm² = 150 cm2. The part of the cube where the hemisphere is attached is not included in the surface area. So, the surface area of the block

= TSA of cube – base area of hemisphere + CSA of hemisphere

= 150 – πr₂ + 2πr₂ + 2πr₂ = (150 πr₂) cm²

.

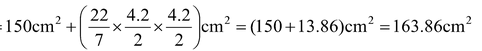Also Check

• Cone
• Cube
• Cylinder

Question 2. A wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)

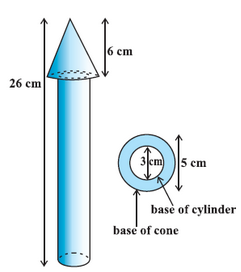
Solution: The radius of cone is denoted by r, slant height of cone by l, height of cone by h, radius of cylinder by r′ and height of cylinder by h′. Then r = 2.5 cm, h = 6 cm, r′ = 1.5 cm, h′ = 26 – 6 = 20 cm and

.

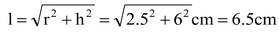Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted.

So, the area to be painted orange

= CSA of the cone + base area of the cone – base area of the cylinder

= πrl + πr₂ – (r’)²

= π [(2.5 × 6.5) + (2.5)² – (1.5)²] cm2

= π [20.25] cm² = 3.14 × 20.25 cm² = 63.585 cm².

Now, the area to be painted yellow = CSA of the cylinder + area of one base of the cylinder

= 2π’r’ + π(r’)²

= πr’h’ + π(r’)²

= (3.14 × 1.5) (2 × 20 + 1.5) cm2 = 4.71 × 41.5 cm²

= 195.465 cm².

Question 3. Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder. If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m3, and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then, how much air is in the shed?

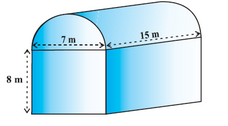
Solution: The volume of air inside the shed (when there are no people or machinery) is given by the volume of air inside the cuboid and inside the half cylinder, taken together. Now, the length, breadth and height of the cuboid are 15 m, 7 m and 8 m, respectively. Also, the diameter of the half cylinder is 7 m and its height is 15 m.

So, the required volume = volume of the cuboids + 1/2 volume of the cylinder

m3 = 1128.75 m³.

Next, the total space occupied by the machinery = 300 m³

And the total space occupied by the workers = 20 × 0.08 m3 = 1.6 m³.

Therefore, the volume of the air, when there are machinery and worker

= 1128.75 – (300.00 + 1.60) = 827.15 m³.

Question 4. A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)

Solution: Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere. The radius BO of the hemisphere (as well as of the cone) = 1/2 x 4cm = 2cm.

So, Volume of the toy

.

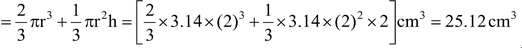Now, let the right circular cylinder EFGH circumscribe the given solid. The radius of the base of the right circular cylinder = HP = BO = 2 cm, and its height is,

EH = AO + OP = (2 + 2) cm = 4 cm.

So, the volume required = volume of the right circular cylinder – volume of the toy

= (3.14 × 22 × 4 – 25.12) cm3 = 25.12 cm³.

Hence, the required difference of the two volumes = 25.12 cm3.

Question 5. A cone of height 24 cm and radius of base 6 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.

Solution: Volume of cone = 1/3 x π x 6 x 24 cm³.

If r is the radius of the sphere, then its volume is 4/3πr³.

Since, the volume of clay in the form of the cone and the sphere remains the same, we have

 4/3 x π x r³ = 1/3 x π x 6 x 6 x 24 i.e., r3 = 3 × 3 × 24 = 32 × 23

So, r = 3 × 2 = 6 .

Therefore, the radius of the sphere is 6 cm.

Question 6. Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)

Solution: The volume of water in the overhead tank equals the volume of the water removed form the sump.

Now, the volume of water in the overhead tank (cylinder) = πr2h = 3.14 × 0.6× 0.6× 0.95 m^3.

The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m³.

The volume of water left in the sump after filling the tank

= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6× 0.6× 0.95)] m³ = (1.57 × 1.44 × 0.95) m³.

So, the height of the water left in the sump

.

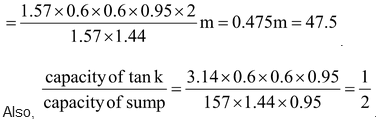Therefore, the capacity for the tank is half the capacity of the sump.

Question 7. A hemispherical tank full of water is emptied by a pipe at the rate of 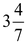litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take π =22 /7)

Solution: Radius of the hemispherical tank = 3/2 m.

Volume of the tank .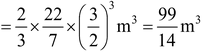

So, the volume of the water to be emptied .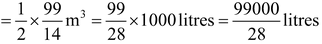

Since, 25/7 liters of water is emptied in 1 second, 99000/28 liters of water will be emptied in 99000/28 x 7/25 seconds, i.e., in 16.5 minutes.

Question 8. A chord of circle 14 cm makes an angle of 60^o at the center of the circle. Find :

(i) area of minor sector (ii) area of the minor segment

(iii) area of the major sector (iv) area of the major segment

Solution: Given, r = 14 cm, θ = 60^o

(i) Area of minor sector OAPB =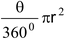

=

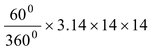
= 102.57 cm^2.

(ii) Area of minor segment APB =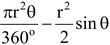

= 102.57 –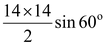

= 102.57 – 98 × √3/2

= 17.80 cm²

(iii) Area of major sector = Area of circle - Area of minor sector OAPB

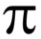= (14)² – 102.57

= 615.44 – 102.57 = 512.87 cm^2.

(iv) Area of major segment AQB

= Area of circle - Area of minor segment APB

= 615.44 – 17.80

= 597.64 cm².

Question 9. ABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semicircle is drawn. Find the area of the shaded portion (figure).

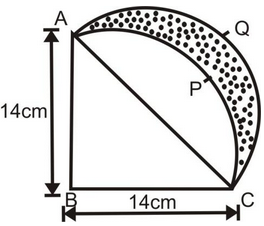
Solution: In right angled triangle ABC,

we have.

AC² = AB² + BC²

AC² = 142 + 142

AC = √2 x 14² = 14√2 cm.

Now required Area = Area APCQA

= Area ACQA – Area ACPA

= Area ACQA - (Area ABCPA - Area of ΔABC)

=

=

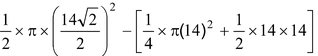
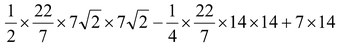
= 154 – 154 98

= 98 cm².

Question 10. The diameter of cycle wheel is 28 cm. How many revolution will it make in moving 13.2 km?

Solution: Distance traveled by the wheel is one revolution = 2πr

= .

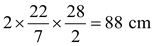and the total distance covered by the wheel = 13.2 × 1000 × 100 cm

= 1320000 cm.

Number of revolution made by the wheel = 1320000/88

= 15000.

Question 11. How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm?

Solution: Volume of the spherical ball of radius 8 cm = .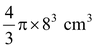

Also, volume of each smaller spherical ball of radius 1 cm =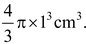

Let n be the number of smaller balls that can be made. Then, the volume of the larger ball is equal to the sum of all the volumes of n smaller balls.

Hence,

⇒ n = 8³ = 512.

Hence, the required number of balls = 512.

Question 12. An iron of length 1 m and diameter 4 cm is melted and cast into thin wires of length 20 cm each. If the number of such wires be 2000, find the radius of each thin wire.

Solution: Let the radius of each thin wire be r cm. Then, the sum of the volumes of 2000 thin wire will be equal to the volume of the iron rod. Now, the shape of the iron rod and each thin wire is cylindrical.

Hence, the volume of the iron rod of radius 4/2  cm = 2 cm is = π x 2² x 100cm²

Again, the volume of each thin wire = πr² x 20

Hence, we have π x 2² x 100 = 2000 x πr² x 20

⇒ 40r² = 4

⇒ r² = 1/100

⇒r = 1/10 [Taking positive square root only]

Hence, the required radius of each thin wire is 1/10 cm. of 0.1 cm.