Division Algorithm For Polynomials
Polynomials of Class 10

FACTOR THEOREM :
Let p(x) be a polynomial of degree greater than or equal to 1 and ‘a’ be a real number such that p(a) = 0. then (x - a) is a factor of p(x). Conversely, if (x - a) is a factor of p(x), then p(a) = 0.
1.Show that x + 1 and 2x - 3 are factors of 2x3 - 9x2 + x + 12.
Sol.To prove that (x + 1) and (2x - 3) are factors of p(x) = 2x - 9x + x + 12 it is sufficient to show that p(–1) and p(3/2) both are equal to zero.
p(–1) = 2(–1) –9(–1) + (–1) + 12 = – 2 – 9 – 1 + 12 = – 12 + 12 = 0
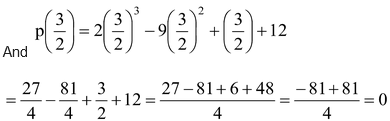
REMAINDER THEOREM:

1.Find the remainder when f(x) = x3 - 6x2 + 2x - 4 is divided by g(x) = 1 - 2x.
Sol.1 - 2x = 0 ⇒ 2x = 1 ⇒ x = 1/2
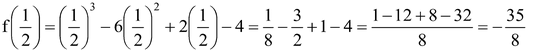
2.Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) = 10x4 + 17x3 - 62x2 + 30x - 3 by b(x) = 2x2 - x + 1.
Sol.
So, quotient q(x) = 5x+ 11 x -28 and remainder r(x) = -9x + 25 .
Now, dividend = Quotient × Divisor + Remainder
= (5x + 11x – 28) (2x – x + 1) + (–9x + 25)
= 10x – 5x + 5x + 22x – 11x + 11x – 56x + 28x - 28 - 9x + 25
= 10x + 17x - 62x + 30x – 3
Hence, the division algorithm is verified.









