Factorisation Quadratic Polynomial
Polynomial of Class 9
FACTORISATION QUADRATIC POLYNOMIAL
For factorisation of a quadratic expression ax2 + bx + a where a ≠ 0, there are two method.
(a) By Method of Completion of Square :
In the form ax2 + bx + c where a ≠ 0, firstly we take ‘a’ common in the whole expression then factorise by converting the expression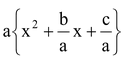 
as the difference of two squares.
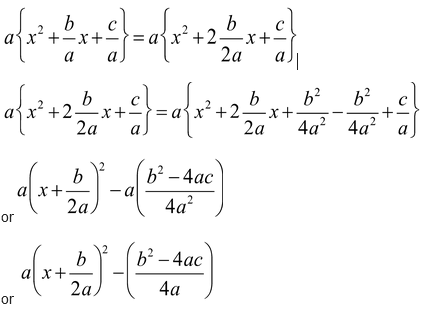
Question Factorize x2– 31x + 220.
Solution: x2– 31a + 220
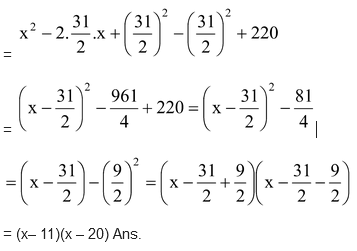
Question Factorize: –10x2 + 31x – 24
Solution:
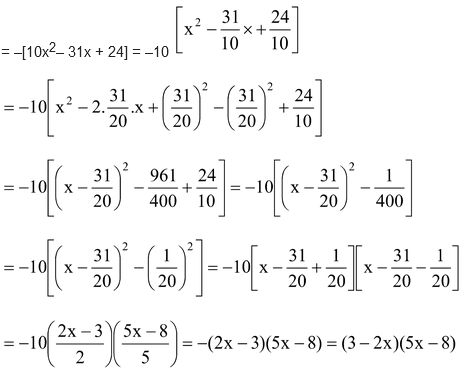
Question 81a2b2c2+ 64a6b2– 144a4b2c
Solution: 81a2b2bc2 + 64a6b2– 144a4b2c
= [9abc] 2– 2 [9abc][8a3b] + [8a3b]2
= [9abc –8a3b]2 = a2b2 [9c – 8a2]2 Ans.
Question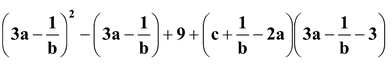 
(b) By Splitting the Middle Term:
In the quadratic expression ax2 + bx + c, where a is the coefficient of x2, b is the coefficient of x and c is the constant term. In the quadratic expression of the form x2 + bx + c, a = 1 is the multiple of x2 and another terms are the same as above.
There are four types of quadratic expression with respect to to the sign change of coefficients of x and constant term :
(i) ax2 + bx + c (ii) ax2– bx + c
(iii) ax2– bx – c (iv) ax2 + bx – c
Splitting middle term of ax2 + bx +c.
In this case, we find integers s and t such that s + t = b and st = ac.
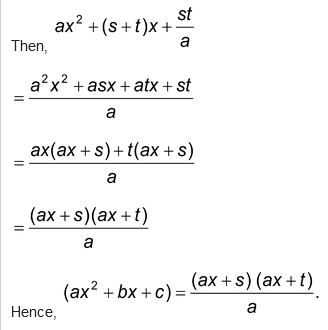
Question Factorize: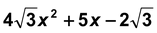 
.
Solution: Here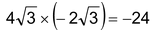 
We try to split 5x into two parts whose sum is 5 and product is = –24
Clearly, 8 + (–3) = 5 and 8 × –3 = –24
Middle term 5x can be written as 8x - 3x
∴
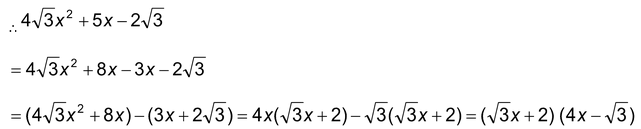
Question Find the value of q, if X + 3 is a factor of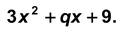 
Solution: Let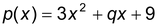 
be the given polynomial. According to question (X+3) is a factor of p(x)
∴ we have p(-3)= 0
⇒ 
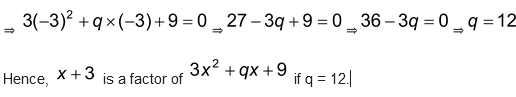
Ex. Factorize: 2x2 + 12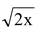
+ 35.
Sol. 2x2 + 12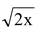 + 35
Product ac = 70 & b = 12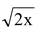
.
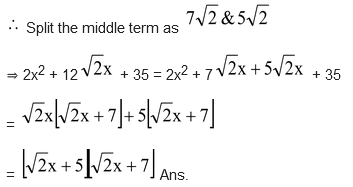Question Factorize: x2 – 14x + 24.
Solution: Product ac = 24 & b = -14
∴ Split the middle term as – 2 &– 2
⇒ x2– 14x + 24 = x2– 12 – 2x + 24
⇒ x(x – 12) – 2 (x – 12) = (x – 12)(x – 2) Ans.
Question Factorize: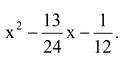 
Solution: 
Product ac = – 48 & b = – 13 ∴ We split the middle term as – 16x + 3x.
=1/24[24x2– 16x + 3x – 2]
=1/24[8x(3x – 2) + 1(3x – 2)]
=1/24(3x – 2)(8x + 1) Ans.
Question Factorize: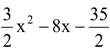
Solution: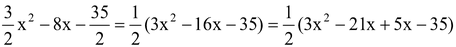 
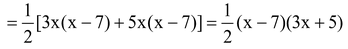Ans.
Question Factorize: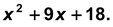 
Solution: The given expression is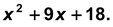
We try to split 9 into two parts whose sum is 9 and product 18.
Clearly, 6 + 3 = 9 and 6 × 3 = 18.
∴ 
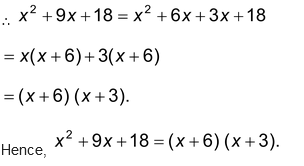
Question Factorize: 
by splitting the middle term:
Solution: In order to factorize we try to split 3√3 into two parts whose sum is 3√3 and product is 6.
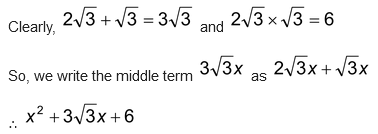
So, we write the middle term 3√3 as 2√3x + √3x
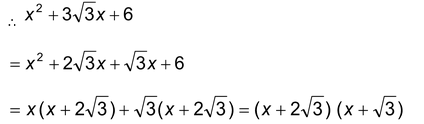
(c) Factorisation by Using the Formula for the Difference of Two Squares:
a2– b2 = ( a + b) (a - b)
Ex. Factorise:4(2a + 3b – 4c) 2– (a – 4b + 5c)2
Solution: = 4(2a + 3b –4c)2– (a – 4b + 5c) 2
= [2(2a + 3b – 4c)]2– (a – 4b + 5c)2
= [4a + 6b – 8c + a – 4b + 5c] [4a + 6b – 8c – a + 4b – 5c]
= [5a + 2b – 3c] [3a + 10b – 13c] Ans.
Question Factorise :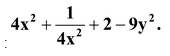
Solution: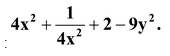
Question Factorize: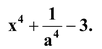 
Solution: 
Ans.
Question Factorize: x4 + x2y2 + y4.
Sol. x2 + x2y2 + y4 = (x2) 2 + 2.x2.y2 + (y2)2– x2y2
= x2 + y2)2– (xy)2
= (x2 + y2 + xy) (x2 + y2– xy) Ans.
(d) Factorization by Using Formula of a3 + b3 and a3– b3:
Ex. Factorize: 64a13b + 343ab13.
Solution: 64a13b + 343ab13 = ab[64a12 + 343b12]
= ab[(4a4)3 + (7b4)3]
= ab[4a4 + 7b4] [(4a4)2– (4a4) (7b4) + (7b4)2]
= ab[4a4 + 7b4][16a8– 28a4b8 + 49b8] Ans.
Question Factorize: p3q2x4 + 3p2qx3 + 3px2 + X/q– q2r3x
Solution: In above question, If we take common then it may become in the form of 3 + b3.
p3q2x4 + 3p2qx3 + 3px2 + X/q– q2r3x
= X/q[p3q3x3 + 3p2q2x2 + 3pqx + 1 – q3r3]
= X/q[(pqx)3 + 3(pqx)2 .1 + 3pqx . (1)2 + (1)3– q3r3]
Let pqx = A & 1 = B
= X/q [A3 + 3A2B + 3AB2 + B3– q3r3]
= X/q[(pqx + 1)3– (qr)3] = X/q[pqx + 1 – qr][(pqx + 1)2 + (pqx + 1) qr + (qr)3]
= X/q[pqx + 1 – qr][p2q2x2 + 1 + 2pqx + pq2xr + qr + q2r2] Ans.
Question Factorize: x3– 6x2 + 32
Solution: x3 + 32 – 6x2
= x3 + 8 + 24 – 6x2
= [(x)3 + (2)3] + 6[4 – x2]
= (x + 2)[x2– 2x + 4] + 6[2 + x][2 – x]
= (x + 2) [x2– 2x + 4 + 6(2 – x)]
= (x + 2)[x2– 2x + 4 + 12 – 6x]
= (x + 2) [x2– 8x + 16]
= (x + 2) (x – 4)2 Ans.
(e) Integral Root Theorem :
If f(x) is a polynomial with integral coefficient and the leading coefficient is 1, then any integer root of f(x) is a factor of the constant term. Thus if f(x) = x3– 6x2 + 11x - 6 has an Integral root, then it is one of the factors of 6 which are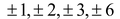 
.
Now Infect f(1) = (1)3– 6(1)2 + 11(1) – 6 = 1 – 6 + 11 – 6 =0
f(2) = (2)3– 6(2)2 + 11(2) – 6 = 8 – 24 + 22 – 6 = 0
f(3) = (3)3– 6(3)2 + 11(3) – 6 = 27 – 54 + 33 – 6 = 0
Therefore Integral roots of f(x) are 1,2,3.
(f) Rational Root Theorem :
Let b/c be a rational fraction in lowest terms. If b/c is a root of the polynomial f(x) =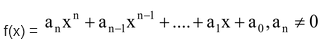 
with integral coefficients. Then b is a factor of constant term a0 and c is a factor of the leading coefficient an.
For example :If b/c is a rational root of the polynomial f(x) = 6x3 + 5x2– 3x – 2, then the values of b are limited to the factors of –2 which are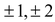 
and the value of c are limited to the factors of 6, which are 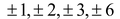Hence, the possible rational roots of f(x) are 
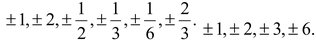Infect -1 is a Integral root and 2/3,-1/2 are the rational roots of f(x) = 6x3 + 5x2– 3x – 2.
NOTE:
(i) An nth degree polynomial can have at most n real roots.
(ii) Finding a zero or root of polynomial f(x) means solving the polynomial equation f(x) = 0. It follows from the above discussion that if f(x) = ax + b, a ≠ 0 is a linear polynomial, then it has only one root given by f(x) = 0 i.e. f(x) = ax + b = 0
⇒ ax = – b
⇒ x =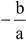 
Thus a= 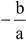is the only root of f(x) = ax + b.
Question If f(x) = 2x3– 13x2 + 17x + 12 then find out the value of f(-2) & f(3).
Solution: f(x) = 2x3– 13x2 + 17x + 12
f(-2) = 2(–2)3– 13(–2)2 + 17 (–2) + 12
= –16 – 52 – 34 + 12 = – 90 Ans.
f(3) = 2(3)3– 13(3)2 + 17(3) + 12
= 54 – 117 + 51 + 12 = 0 Ans.
(f) Factorisation of an Expression Reducible to a Quadratic Expression :
Question Factorize:- 8 + 9(a – b)6– (a – b)12
Solution: –8 + 9(a –b)6– (a – b)12
Let (a –b)6 = x
Then –8 + 9x – x2 = – (x2– 9x + 8) = – (x2– 8x – x + 8)
= – (x– 8)(x – 1)
= – [(a– b)6– 8][(a – b)6– 1]
= [1 – (a –b)6][(a – b)6– 8]
= [(1)3– {(a – b)2}3][{(a – b)2}3– (2)3]
= [1 – (a –b)2][1 + (a – b)4 + (a – b)2][(a – b)2– 2][(a – b)4 + 4 + 2(a – b)2] Ans.
Question Factorize: 6x2– 5xy – 4y2 + x + 17y – 15
Solution: 6x2 + x[1 – 5y] – [4y2– 17y + 15]
= 6x2 + x[1 – 5y] – [4y2– 17y + 15]
= 6x2 + x[1 – 5y] – [4y(y – 3) – 5(y – 3)]
= 6x2 + x[1 – 5y] – (4y – 5)(y – 3)
= 6x2 + 3(y –3)x– 2(4y – 5)x – (4y –)(y - 3)
= 3x[2x + y 3] - (4y - 5)(2x + y - 3)
= (2x + y - 3)(3x - 4y + 5) Ans.
