Polynomials types

POLYNOMIALS

We have already studied the algebraic expressions, their addition of algebraic expression, subtraction of algebraic expression , multiplication and division of algebraic expressionin previous classes.Now we have to move ahead and study polynomials.

(x + y)² = x² + 2xy + y²

(x – y)² = x² – 2xy + y²

and x² – y² = (x + y) (x – y)

Now, we will study a particular type of algebraic expression, called polynomial. We also study the remainder theorem and factor theorem.

Polynomial is an algebraic expression having one or more terms involving powers of the variable.

An expression p(x) of the form:

where all 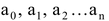are real numbers and n is non-negative integer (i.e. whole numbers) is called a polynomial of degree n when 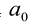is not equal to zero.

For example,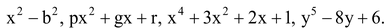

If the power of x or y be in either increasing or decreasing order, the polynomial in x or y is said to be in standard form.

∴

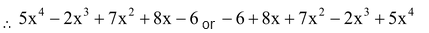
TERMINOLOGY BEFORE UNDERSTANDING POLYNOMIALS 

The algebraic expressions having only one variable like 2x, 3a, –b, -3/5x etc.

We can see in the above algebraic expressions each term contain (a constant) × (a variable).

Like in 2x - 2 is a constant and x is a variable ,similarly 3 is a constant) × a (a variable), –1(a constant) × b (a variable), -3/5 (a constant) × x(a variable).

From the above example we can understand the different terminology like-

Variable :

A symbol has any real value is called variable. 

In the given example x, a, b are variables.

(ii) Constant :A symbol with a fixed numerical value is called constant.

In the given example 2, 3, -1, -3/5 are constants.

(iii) Terms :

In a polynomial 2x² + 5x + 11, the expression 2x², 5x and 11 are called the terms of the polynomial.

Here, the number of terms is 3. But, the number of terms in 5x⁶ + 2x⁴ + 3x³ + 2x² – 6x + 10 is 6

(iv) Coefficient :

Each term of a polynomial has a coefficient. Hence, 6x⁴ + 5x³ – 8x + 19, the coefficient of x4 is 6, the coefficient of x³ is 5, the coefficient of x is
–8 and 19 is the coefficient of x0or constant term. (Constant term means x0 = 1)

(v) Zero polynomial :

A polynomial consisting of one term, namely zero only, is called a zero polynomial. The degree of zero polynomial is not defined.

(vi) Monomials

Polynomials having only one term are called monomials e.g.

(vii) Binomials

Polynomials having only two terms are called binomials e.g. x+1, .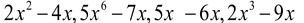

(viii) Trinomials

Polynomials having only three terms are called trinomials e.g. ,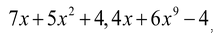 

(ix) Multinomial

Polynomials having only three terms are called trinomials e.g.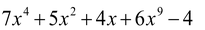

question Which of the following expressions are polynomials?

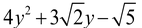(i) (ii) (iii)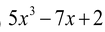

(iv) (v)

Solution: (i) is an expression having only non-negative integral powers of x. So, it is a polynomial.

(ii) 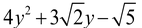is an expression having only non-negative integral power of y. So, it is a polynomial.

(iii) 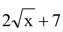is an expression in which one term, namely 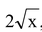has rational power of x. So, it is not a polynomial.

(iv) is an expression having only non-negative integral powers of t. So, it is a polynomial in t.

(v) The given expression may be written as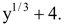

It contains a term containing rational power of y. So, it is not a polynomial.

Related Topics 

• Factorisation Quadratic Polynomial
• Remainder Theorm

DIFFERENT TYPES OF POLYNOMIALS:

Generally, we divide the polynomials in the following categories.

(i) Based on degrees:

There are four types of polynomials based on degrees. These are listed below :

(A) Linear Polynomials: A polynomials of degree one is called a linear polynomial. The general formula of linear polynomial is ax + b, where a and b are any real constant and a ≠ 0.

(B) Quadratic Polynomials: A polynomial of degree two is called a quadratic polynomial. The general form of a quadratic polynomial is ax2 + b + c, where a ≠ 0.

(C) Cubic Polynomials: A polynomial of degree three is called a cubic polynomial. The general form of a cubic polynomial is ax3 + bx2 + cx + d, where a ≠ 0.

(D) Biquadratic (or quadric) Polynomials: A polynomial of degree four is called a biquadratic (quadratic) polynomial. The general form of a biquadratic polynomial is ax4 + bx3 + cx2 + dx + e , where a ≠ 0.

Things to remember 

A polynomial of degree five or more than five does not have any particular name. Such a polynomial usually called a polynomial of degree five or six or ....etc.

(ii) Based on number of terms

There are three types of polynomials based on number of terms. These are as follows :

(A) Monomial: A polynomial is said to be monomial if it has only one term. e.g. x, 9x², 5x³ all are monomials.

(B) Binomial: A polynomial is said to be binomial if it contains two terms e.g. 2x2 + 3x, √3x + 5x³, – 8x³ + 3, all are binomials.

(C) Trinomials :A polynomial is said to be a trinomial it if contains three terms. e.g. 3x³ - 8 +5/2,

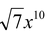8x⁴ - 3x², 5 - 7x + 8x9, are all trinomials.

Things to remember 

A polynomial having four or more than four terms does not have particular Name. These are simply called polynomials.

question Give one example each of a binomial of degree 61 and a monomial of degree 23.

Solution: (i) A binomial of degree 61 is 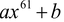for all ‘a’ is non-zero real number and a is called coefficient of 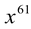also b≠ 0. One such example is

(ii) A monomial of degree 23 is 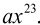for all ‘a’ in a non-zero real number ‘a’ is called coefficient of One such example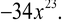

question Classify the following as linear, quadratic and cubic polynomials:

(i) 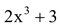(ii) 4t (iii)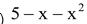

Solution: (i) 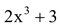is a polynomial of degree 3. So, it is a cubic polynomial.

(ii) 4t is a polynomial of degree 1. So, it is a linear polynomial.

(iii) Arranging in standard form .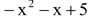

It is a polynomial of degree 2. So, it is a quadratic polynomial.

(iii) Zero degree polynomial :Any non-zero number (constant) is regarded as polynomial of degree zero or zero degree polynomial. i.e. f(x) = a, where a 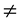0 is a zero degree polynomial, since we can write f(x) = a as f(x) = ax0.

(iv) Zero polynomial :A polynomial whose all coefficients are zeros is called as zero polynomial i.e. f(x) = 0, we cannot determine the degree of zero polynomial.

• An expressionp(x) = a₀x_n + a₁x_n – 1 + a₂x_n – 2 + a_n is a polynomial

• Where a₀, a₁, ………..an are real numbers and n is non-negative integer.

• Degree of a polynomial is the greatest exponent of the variable in the polynomial.

•  Constant polynomial is a polynomial of degree zero. The constant polynomialf(x) = 0 is called zero polynomial.
• Degree of zero polynomial is not defined.

REMAINDER THEOREM

Let P(x)  is a polynomial of degree greater than or equal to 1 and a is any real number, if p(X) is divided by the linear polynomial  x-a  then the remainder is P(a);