Equations of Higher Degree

Equations of Higher Degree

An equation of degree n can be represented

as F(x) = a₀x_n + a₁x_n-1 + a₂x_n-2 + . . . + a_n = 0

with a₀, a₁, a₂ . . . an ∈ C and a₀ ≠ 0.

Then F(x) can be expressed as F(x) = a₀ (x-α¹) (x-α²) . . . (x-α_n) implying that it will have exactly n roots (No more, no less)

Also the roots are connected by the relations α1 + α2 + … + αn =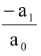

Σ α₁α₂ = 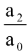Σ α₁α₂α₃ = -etc.

For example if α, β, γ are the roots of a cubic equation ax³ + bx2 + cx + d = 0

Then α + β + γ = , αβ + βγ + γα = and αβγ = -.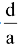

This situation prevails in equations of any finite degree.