Nature of roots

Nature of Roots

I Suppose, a,b,c ∈ R a ≠ 0. Then the following points are worth noting

(a) The given equation has real and distinct roots if and only if D>0.

(b) It has real and equal roots if D = 0.

(c) It has complex roots with non zero imaginary parts if D < 0.

Note:  Imaginary roots occur in conjugate pair.

II If a,b,c ∈ Q and p+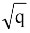 is an irrational root of the equation ax² + bx + c = 0, then p - 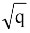is the other root of the equation.

III If a = 1, b, c ∈ I and the roots of the given equation are rational numbers, then these roots must be integers.

IV If the equation ax² + bx + c = 0 is satisfied by more than 2 values of x, then it must be an identity. i.e. a = 0, b = 0 and c = 0.