Application Of Quadratic Equations

1. Translate the word problem into symbolic language and formulate the quadratic equation.

2. Solve the quadratic equation formed in above step.

3. Translate the solution into verbal language and ignore the solution which does not have a meaning for the problem.

REMARKS:

• Two consecutive odd natural numbers be 2x – 1, 2x + 1 where x ∈ N
• Two consecutive even natural numbers be 2x, 2x + 2 where x ∈ N
• Two consecutive even positive integers be 2x, 2x + 2 where x ∈ Z⁺
• Consecutive multiples of 5 be 5x, 5x + 5, 5x + 10 .....

question 1. The sum of the squares of two consecutive positive integers is 545. Find the integers.

Solution: Let x be one of the positive integers. Then the other integer is x + 1, x ∈ Z⁺

Since the sum of the squares of the integers is 545, we get

x² + (x + 1)2 = 545

or 2x² + 2x – 544 = 0

or x² + x – 272 = 0

x² + 17x – 16x – 272 = 0

or x(x + 17) – 16(x + 17) = 0

or (x – 16) (x + 17) = 0

Here, x = 16 or x = –17 But, x is a positive integer. Therefore, reject x = –17 and take x = 16. Hence, two consecutive positive integers are 16 and (16 + 1), i.e., 16 and 17.

question 2. The length of a hall is 5 m more than its breath. If the area of the floor of the hall is 84 m2, what are the length and the breadth of the hall?

Solution: Let the breadth of the hall be x metres.

Then the length of the ball is (x + 5) metres.

The area of the floor = x(x + 5) m²

Therefore, x(x + 5) = 84

or x² + 5x - 84 = 0

or (x + 12) (x - 7) = 0

This given x = 7 or x = –12.

Since, the breadth of the hall cannot be negative, we reject x = –12 and take x = – only.

Thus, breadth of the hall = 7 metres, and length of the hall = (7 + 5), i.e., 12 metres.

question 3. The sum of two numbers is 15. If the sum of their reciprocals is 3/10, find the numbers.

Solution: Let the required numbers be x and 15 – x. Then,

According to question, we have

⇒ x = 10 or, x = 5

Hence, the two numbers are 10 and 5.

question 4. A two-digit number is such that the product of its digits is 14. When 45 is added to this number, the digits interchange their places. Find the number.

Solution: Let the tens digit be x then the units digit  = 14/x

Then, the two digit number is .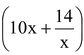

Reverse number =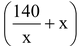

According to question, we have

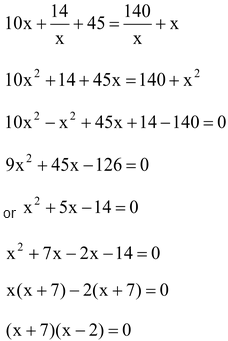
x = 2; x = - 7 is rejected as digit cannot be negative

∴ x = 2 and other digit  = 14/2 = 7

Hence, the required number is 10 × 2 + 7 i.e. 27.