
Median
Statistics of Class 10
Median is the center or middle value in a given set of numbers or data. In mathematics, three measures are used to find the average value for a given set of numbers. They are mean, median, and mode. These three measures are called measures of central tendency. The average gives the average value of the provided data. The median defines the mean value of the given data. The mode determines the repeated value of the given data. Here we will discuss one of the measures called the "median." The definition of median, its formula, and examples are explained.
| Table of Content |
What is Median?
A median is one of three measures of central tendency. When describing a data set, the middle position of the given data set is identified. This is defined as the measure of central tendency. The three most common measures of central tendency are the mean, median, and mode.
Definition
In maths, the median is defined as the middle value of an ordered list of numbers. Find the middle number by lining up the numbers. The numbers are sorted in ascending order. Once the numbers are arranged, the middle number is called the median of the data set.
Median Formula for Grouped Data
The median is calculated using the following steps when the data are continuous and in the form of a frequency distribution.
- Step 1: Find the total no. of observations denote by n.
- Step 2: Define the class size (h) and then divide the data into different classes.
- Step 3: Find the cumulative frequency of each class.
- Step 4: Determine the class the median falls into. (The middle class is the class where n/2 lies.)
- Step 5: Find the lower bound of the median class (l) and the cumulative frequency of the class preceding the median class (c).

How to Find the Median?
We use the median formula to find the mean value of the given data. We can find the mean for a set of ungrouped data by following the steps below.
- Step 1: Place the given data in ascending order.
- Step 2: Count the total number of observations.
- Step 3: If the given number of observations is odd, then, use the formula: Median = [(n + 1)/2]th term
- Step 4: If the given number of observations is even, use the formula: Median = [(n/2)th term + (n/2 + 1)th term]/2
Raw Data of Median
- Arrange the data in ascending order.
- Count the no. of observation (Let there be ‘n’ observation)
-
If n be odd then median = value of
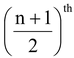 observation.
observation. -
If n is even then median is the arithmetic mean of (n/2) observation and
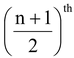 observation.
observation.
Advantages of Median
- It is rigidly defined, easily, understood and calculate.
- It is not all affected by extreme values.
- It can be located graphically, even if the class - intervals are unequal.
- It can be determined even by inspection is some cases.
Disadvantages of Median
- In case of even numbers of observations median cannot be determined exactly.
- It is not based on all the observations.
- It is not subject to algebraic treatment.
- It is much affected by fluctuations of sampling.
Uses of Median
- Median is the only average to be used while dealing with qualitative data which cannot be measured quantitatively but can be arranged in ascending or descending order of magnitude.
- It is used for determining the typical value in problems concerning wages, distribution of wealth etc.
Solved Example
Q1. Following are the lives in hours of 15 pieces of the components of aircraft engine. Find the median:
715, 724, 725, 710, 729, 745, 649, 699, 696, 712, 734, 728, 716, 705, 719
Ans. Arranging the data in ascending order
644. 696, 705, 710, 712, 715, 716, 719, 724, 725, 728, 729, 734, 745
N = 15
So, Median =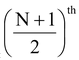 observation
observation
= (15 + 1/2)th observation
= 716.
Median of class-interval data (Grouped)
Median = l + [(n/2−c)/f] × h
l = lower limit of median class,
N = total no of observation
C = cumulative frequency of the class preceding the median class
h = size of the median class
f = frequency of the median class.
Q2. Find the median wage of a worker for the above date.
| Daily wages (in Rs.) | No. of workers | Cumulative frequency |
| 125 | 6 | 6 |
| 130 | 20 | 26 |
| 135 | 24 | 50 |
| 140 | 28 | 78 |
| 145 | 15 | 93 |
| 150 | 4 | 97 |
| 160 | 2 | 99 |
| 180 | 1 | 100 |
N = 100 (even)

= 137.50
Frequently Asked Question (FAQs)
Q1. What does n represent in Median Formula?
Ans. In the median formula, 'n' represents the number of observations. When 'n' is odd then the median formula is [Median = {(n + 1)/2} term]. When 'n' is even then the median formula is [Median = ((n/2) term + (n/2 + 1)th term)/2].
Q2. What is a median class in statistics?
Ans. The median class is defined as the class interval whose cumulative frequency is greater than (and nearest to) n/2.
Q3. What is a median number in math?
Ans. The median is known as the middle number in a sorted, ascending, or descending list of numbers that can be more descriptive of the data set than the average.
