Congruent And Similar Figures

Two geometric figures having the same shape and size are known as congruent figures. Geometric figures having the same shape but different sizes are known as similar figures.

SIMILAR TRIANGLES:

Two triangles ABC and DEF are said to be similar if their

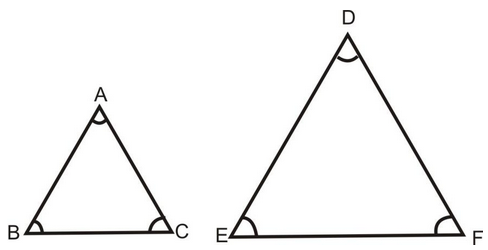
(i) Corresponding angles are equal.

i.e. ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

And,

(ii) Corresponding sides are proportional

i.e. .

CHARACTERISTIC PROPERTIES OF SIMILAR TRIANGLES :

(i) (AAA Similarity) If two triangles are equiangular, then they are similar.

(ii) (SSS Similarity) If the corresponding sides of two triangles are proportional, then they are similar.

(iii) (SAS Similarity) If in two triangle’s one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.

RESULTS BASED UPON CHARACTERISTIC PROPERTIES OF SIMILAR TRIANGLES:

(i) If two triangles are equiangular, then the ratio of the corresponding sides is the same as the ratio of the corresponding medians.

(ii) If two triangles are equiangular, then the ratio of the corresponding sides is same at the ratio of the corresponding angle bisector segments.

(iii) If two triangles are equiangular then the ratio of the corresponding sides is same at the ratio of the corresponding altitudes.

(vi) If one angle of a triangle is equal to one angle of another triangle and the bisectors of these equal angles divide the opposite side in the same ratio, then the triangles are similar.

(v) If two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and the corresponding median of another triangle, then the triangles are similar.

(vi) If two sides and a median bisecting the third side of a triangle are respectively proportional to the corresponding sides and the median another triangle, then two triangles are similar.

Do solve NCERT text book for class 10 maths with the help of Physics Wallah (PW) NCERT solutions for class 10 maths.