Square Relation
Trigonometry of Class 10
THEOREM 2:
For any acute angle θ, prove that
(i)  ;
;
(ii) 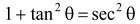 ;
;
(iii) 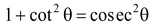 .
.
|
Proof: Consider a right-angle ΔPQR in which ∠Q = 90º and ∠P = θº. Let PQ = x units, RQ = y units and PR = z units. Then, by Pythagoras' theorem, we have
|
|
Now, (i)

[∴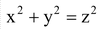 ]
]
∴  .
.
(ii) 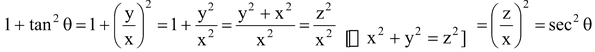 .
.
∴ 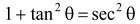 .
.
(iii) 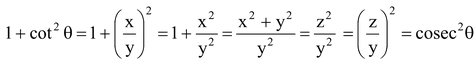
[∴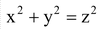 ]
]
∴ 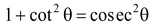 .
.
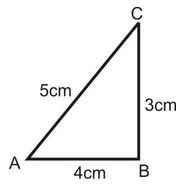
Q1. In the given triangle AB = 3 cm and AC = 5 cm. Find all trigonometric ratios.
Solution: Using Pythagoras theorem,
AC2 = AB2 + BC2
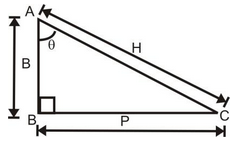
⇒ 52 = 32 + P2
⇒ 16 = P2 ⇒ P = 4 cm
Here P = 4 cm, B = 3 cm, H = 5 cm
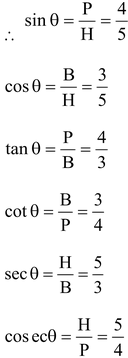
question 2. If tan θ = m/n, then find sin θ.
Solution: Let P = mα and B = nα
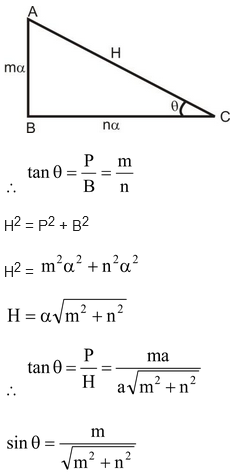
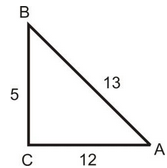
Q3. If cosec A = 13/5 , the prove that tan2 A – sin2 A = sin4 A sec2 A.
Solution: We hare cosec A = 13/5 = Hypotenuse/Perpendicular.
So, we draw a right triangle ABC, right angled at C such that hypotenuse AB = 13 units and perpendicular
BC = 5 units.
By Pythagoras theorem,
AB2 = BC2 + AC2  (13)2 = (5)2 + AC2
(13)2 = (5)2 + AC2
AC2 = 169 – 25 = 144
AC = √144 = 12 units

L.H.S. tan2 A – Sin2 A R.H.S. = sin4 A × sec2 A
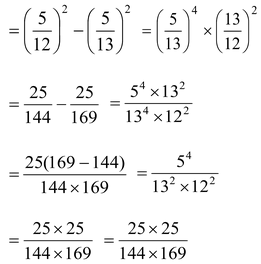
So, L.H.S. = R.H.S. Hence, proved.
Q4. In ΔABC, right angled at B, AC + AB = 9 cm. Determine the value of cot C, cosec C, sec C.
Solution: In Δ ABC, we have
(AC)2 = (AB)2 + BC2
⇒ (9 – AB)2 = AB2 + (3)2 [ AC + AB = 9cm ⇒ AC = 9 – AB]
⇒ (81 + AB2 – 18AB = AB2 + 9
⇒ 72 – 18 AB = 0
⇒ AB = 72/18 = 4cm
Now, AC + AB = 9 cm
AC = 9 – 4 = 5 cm.
So, cot C = BC/AB = 3/4,cosec C = AC/AB = -5/4,sec C = AC/BC = 5/3.
Q5. Given that cos (A – B) = cos A cos B + sin A sin B, find the value of cos 15o.
Solution: Putting A = 45o and B = 30o, we get
we get cos (45o – 30o) = cos 45o cos 30o + sin 45o sin 30o
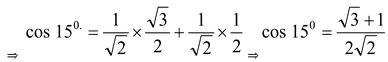
Q6. Evaluate:
(i) sin 60º cos 30º – cos 60º sin 30º
(ii) tan 30º cosec 60º + tan 60º sec 30º
Solution: (i) sin 60º cos 30º – cos 60º sin 30º
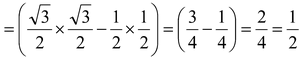 .
.
(ii) tan 30º cosec 60º + tan 60º sec 30º
question 7. Evaluate:
(i) 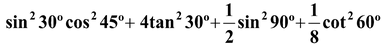
(ii) 
Solution:
(i) 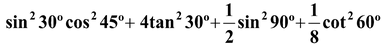
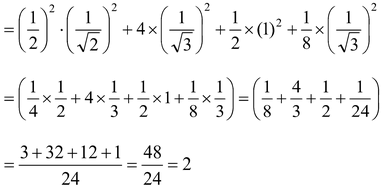
(ii) 
 .
.
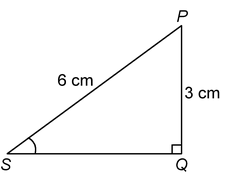
Q8. In ΔPQS, right-angled at Q, PQ = 3 cm and PS = 6 cm. Determine ∠QPS and ∠PSQ.
|
Sol. Given PQ = 3 cm and PS = 6 cm.
∴
or So, ∠PSQ = 30º and ∴ ∠QPS = 60º. |
|
Q9. If sin (A – B) = 1/2, cos (A + B) = 1/2, 0º < A + B ≤ 90º, A > B, find A and B.
Solution: Since, sin (A – B) = 1/2
or sin(A - B) = sin30°
therefore, A – B = 30º. ... (i)
Also, since cos (A + B) = 1/2
or cos(A + B) = cos60°
therefore, A + B = 60º. ... (ii)
Adding (i) and (ii), we have A = 45º and B = 15º.
Frequently Asked Question
Q1. What is Square relation in trigonometry?
Ans. Square relations among various trigonometrical ratios
sin2θ+cos2θ=1. sec2θ−tan2θ=1. cosec2θ−cot2θ=1. These are also called Pythagorean Identities.
Q2. What are the formulas of trigonometry class 10?
Ans. Class 10 Trigonometry Formulas
sin(90° - A) = cos A
cos(90° - A) = sin A
tan(90° - A) = cot A
cot(90° - A) = tan A
sec(90° - A) = cosec A
cosec(90° - A) = sec A
sin2 θ + cos2 θ = 1 ⇒ sin2 θ = 1 - cos2 θ ⇒ cos2 θ = 1 - sin2 θ
cosec2 θ - cot2 θ = 1 ⇒ cosec2 θ = 1 + cot2 θ ⇒ cot2 θ = cosec2 θ - 1.
Q3. How do you do Class 10 trigonometry easily?
Ans. 7 Easy Steps to Learn Trigonometry
- Study all the basics of trigonometric angles.
- Study right-angle triangle concepts.
- Pythagoras theorem.
- Sine rule and Cosine rule.
- List all the important identities of trigonometry.
- Remember the trigonometry table.
- Be thorough with the trigonometric formulas.
Q4. Is trigonometry important for JEE?
Ans. Trigonometry: It is one of the most important topics for JEE Main. Inverse Trigonometry, Trigonometric functions, trigonometric ratios and trigonometric identities are some of the most imperative topics where you need to focus on.
Q5. Why is trigonometry so hard?
Ans. With trigonometry, you have to remember what sine and cosine mean, for example. You have to remember what they represent and the various ways they impact angles and lengths. Trigonometry is difficult because it involves a lot of memorization of different functions which can then deviate into other functions.
Q6. What is relation between Sinθ and Cosecθ?
Ans. Reciprocal Relationship
As the name suggests, these relations involve two trigonometric ratios which are connected by inverse relations between them. For example, sin θ = 1/ cosec θ or sin θ x cosec θ = 1. cos θ = 1/ sec θ or cos θ x sec θ = 1.
Q7. What is the relation between tanθ and cotθ?
Ans. The Tanθ is the ratio of the altitude, base of the right triangle, and Cotθ is the ratio of the base, altitude of the right triangle. The cot - tan formula presents an inverse relationship between Cotθ and Tanθ.
.png)
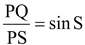
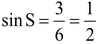 .
.